Celdas y trayectorias imposibles

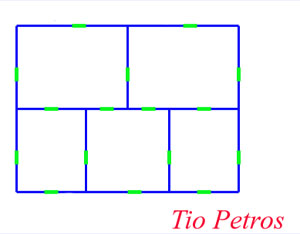Tenemos en la ilustración un conjunto de cinco celdas agrupadas de una manera concreta. Podemos pensar que es el plano de una vivienda.Cada pared interconecta una celda con otra contigua, o con el exterior mediante una puerta, en verde en el dibujo. Se trata de encontrar una trayectoria que atraviese todas y cada una de las puertas(dieciseis en total)una sola vez.

Tras unos cuantos intentos, vereis que no es fácil encontrar la solución. Es el momento de preguntarse si será imposible. Una de las formas de resolver el enigma es revisar exhaustivamente todas las posibilidades, de la misma forma que se demostró el Teorema de los cuatro colores . Es una demostración perfectamente válida, pero espantosamente fea. Además, con este problema, no valdría para demostrar nada con una composición de celdas más complicada: habría que empezar desde el principio otra vez.

Así pues, lo más elegante sería demostrar que tal trayectoria es imposible en nuestra figura, comprendiendo los porqués de tal imposibilidad. Es, como muchas cosas en matemáticas, increíblemente fácil una vez se comprende el asunto, pero sé por experiencia que mucha gente se queda atascada.

Una vez comprendido el asunto, nada cuesta responder a la misma pregunta en composiciones más complicadas.

¿Les apetece pensarlo?

Si les apetece les aconsejo coger un papel e intentar trayectorias: no tardarán en desesperarse . Es mucho mejor que intenten ver porqué no puede existir tal trayectoria

14 comentarios

[Eduardo - 17 de febrero de 2004 - 18:05]

Me hago eco de las palabras de Vailima. Un chileno que ama las matematicas.

[Vailima - 17 de febrero de 2004 - 09:46]

Tio Petros ¿acaso te has quedado encerrado en una de tus celdas?
Por favor, escribe.
Un saludo

[ToReK - 11 de febrero de 2004 - 23:48]

En http://kirai.webcindario.com/ comento como solucionar el problema usando grafos. Saludos

[Shunt - 11 de febrero de 2004 - 08:21]

Muy agudo. Esa es una condición necesaria, pero no suficiente. De estas otras, se podría enunciar alguna?

[Crystal - 10 de febrero de 2004 - 22:31]

Chapó!;P esto está poniéndose cada vez más interesante, pero voy a tener que recuperar clases (ya queda poco...)

[mig21 - 10 de febrero de 2004 - 13:59]

Tienes razón Tío, no era tan difícil...
Pero es que justo ayer leí que fué Euler el que resolvió el problema y claro, es mucho Euler :)

Saludos

[Tio Petros - 10 de febrero de 2004 - 13:57]

Sí.

[Tute - 10 de febrero de 2004 - 13:18]

Wow... ¿le pegué?

[Tio Petros - 10 de febrero de 2004 - 13:09]

Hola Mig. No es para tanto.
La respuesta de Tute es muy acertada.
Todo se basa en una observación aparentemente trivial: desde la perspectiva de cualquiera de las celdas, atravesar una de sus puertas supone cambiar de situación respecto a la misma: si se estaba dentro, ahora se está fura y viceversa. ¿Sí?

Pues bien: pasar un número impar de puertas supone igualmente cambiar de situación respecto a una celda. Como tres de las celdas tienen cinco puertas, si empezamos el tour dentro de una concreta de las tres, debemos acabar fuera de ella necesariamente, y si empezamos fuera de una concreta de ellas, debemos indefectiblemente terminar dentro de la misma. El mismo razonamiento vale para las tres,lo cual es absurdo: sólo podemos terminar dentro de una celda. Por eso es imposible con más de dos celdas con número impar de puertas cumplir lo pedido en el enunciado.

¿A que era simple?

No hacen falta conocimientos de topología, ni de historia de la matematica, ni de geografía antigua de la ciudad de Königsberg...

[mig21 - 10 de febrero de 2004 - 09:23]

¿Te estas leyendo Linked?(yo si, tremenda coincidencia, o no...)
¿crees que somos Euler? :)(Aunque Tute casi lo es....)
¿Deberíamos pasarnos por Könisberg?
Saludos :)

[Tute - 09 de febrero de 2004 - 23:56]

Gran error el mío, corrección en el 3er item:

-de lo contrario, cada vez que entre debo salir; es decir: necesito una cantidad par de puertas.

Mis disculpas

[Tute - 09 de febrero de 2004 - 23:54]

No me he sentado a pensarlo detenidamente pero intuyo lo siguiente:

-Tiene que ver con la cantidad de puertas de cada habitación.
-Si la habitación es punto de partida o de llegada puede tener una cantidad impar de puertas.
-de lo contrario, cada vez que entre debo salir; es decir: necesito una cantidad impar de puertas.

Entonces, según lo que acabo de decir (de lo que no estoy seguro) tendría que haber 2 o menos habitaciones con cantidad impar de puertas. Si hay 2 entonces una es de partida y la otra de finalización del recorrido; por simetría sería indistinto. Si hay una sola, entonces comienza 'dentro' de la casa en esa habitación y termina fuera (o al revés).
Si no hay ninguna entonces comienzo y termino afuera; lo que podría traducir como que el circuito es cerrado y puedo comenzar en cualquier habitación y terminar en ella.

Estoy diciendo sandeces ¿no?

[Tio Petros - 09 de febrero de 2004 - 21:59]

Sé que es broma. Además, quien aquí entra lo hace por placer, verdad? ;-)
Por lo que al problema respecta, no gastes más folios: es imposible. El reto es encontrar la demostración, y para eso no hace falta ni siquiera tomar el lápiz.

[Rimblow - 09 de febrero de 2004 - 19:41]

Como yo bien sospechaba, quieres acabar con nosotros, deseas que quememos nuestras pobres neuronas y las llevemos hasta límites insospechados,.....lo estás logrando,.....,pueder ser que alguien se anime y te ponga a ti algún "problemilla", más que nada para que partamos todos igual, no por otra cosa..........

P.D. Sabes que es broma, y me encanta que nos piques un poquillo, te aliento a que sigas a si, por siempre jamás...un saludo a tod@s.

P.D.2. Ya he gasta un folio por las dos caras, y nada de nada...