Mundos extraños
 Estamos en condiciones para apreciar las diferencias entre la topología usual y otras topologías más, digamos, exóticas. Sabemos que un mismo conjunto, un plano por ejemplo, con dos topologías diferentes forma dos espacios topológicos diferentes en los que ocurrirán cosas deferentes.
Estamos en condiciones para apreciar las diferencias entre la topología usual y otras topologías más, digamos, exóticas. Sabemos que un mismo conjunto, un plano por ejemplo, con dos topologías diferentes forma dos espacios topológicos diferentes en los que ocurrirán cosas deferentes. Vamos a definir una topología diferente a la usual en el plano. Recordamos que la usual es la que tiene los abiertos formados por uniones arbitrarias de bolas abiertas. Los entornos de un punto los podemos visualizar perfectamente como discos centrados en dichos puntos, tan grandes o pequeños como queramos. En realidad los posibles entornos de un punto serán muchos más que los anteriores: todos los subconjuntos del plano que contengan a un abierto de la topología, y por supuesto que contenga al punto considerado. No voy a escribir la frase anterior cada ver que hable de entornos de un punto, de forma que considero que a partir de aquí se entiende.
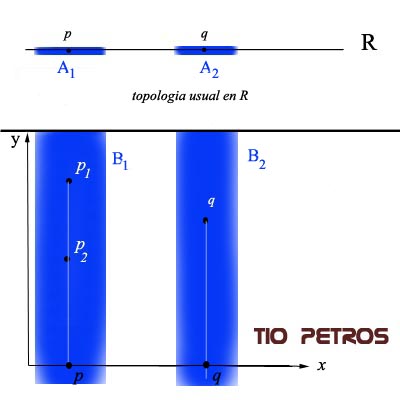
Tomemos la topología usual en la recta. La tienen en la parte superior de la figura. Dos puntos, p y q con dos entornos suyos: dos intervalos abiertos que contienen a los puntos respectivamente. El plano es el producto cartesiano de R por sí mismo. Para cada abierto A de la topología de la recta, consideraremos el subconjunto del plano siguiente:
BA={(x,y) R2 tal que x A ; y R}
Esto es: cada abierto de R define uno y solo un abierto en R2, que son las bandas infinitas hacia arriba y hacia abajo de la parte inferior de la figura; cuyos valores en el eje X corresponden a las respectivos de los entornos de R de los cuales derivan. Es fácil demostrar que se trata efectivamente de una topología, pues sus propiedades dimanan directamente de las de la topología usual de R.
Este topología de R2 es tan fina como la usual de R, pero en R2 hay muchos más puntos que discriminar. No debemos extrañarnos que pasen cosas extrañas.
Para empezar; los puntos p1 y p1 tienen la misma componente x, luego todo entorno de uno de ellos engloba al otro. Olvidémonos de que los entornos eran disquitos que dibujábamos alrededor de los puntos: ahora un entorno es una banda vertical infinita de grosor cualquiera, o una suma arbitraria de bandas de este estilo!!!
La topología dada es demasiado grosera para separar todos los puntos del espacio en cuestión (plano).
Definimos un espacio topológico como espacio de Haussdorf o espacios de tipo T2 cuando dados dos puntos diferentes del mismo, es posible encontrar un entorno de cada uno de ellos de forma que ambos tengan intersección nula ( que no se toquen, vaya). En nuestro ejemplo esto sólo es posible si los puntos considerados tienen valor de x diferente. Si la tienen igual, todo entorno de uno de ello cortará a todo entorno del otro. No es un espacio de Haussdorf.
Qué pasa en dicho espacio con un círculo como el de la figura?

Pues que tiene interior vacío!
Efectivamente, definíamos el interior como el conjunto de puntos para los cuales existía algún entorno totalmente incluido en el conjunto. Esto no es posible para el círculo en este espacio; todos los puntos aparentemente interiores en realidad son puntos de la frontera , pues cualquier entorno de los mismos tiene tanto puntos del círculo como puntos del complementario del círculo.
Una vez más, la intuición nos falla. Y es que en espacios como este las cosas son muy diferentes de las habituales...
Nuestra idea intuitiva del continuum de números relaes en la recta, o de puntos del plano o espacio tridimensional obedece a un espacio topológico T2 . De ahí que las cosas que ocurren en espacios que no son de Haussdorf, nos desconciertan a veces. Se trata desde nuestra perspectiva de mundos ciertamente extraños.
5 comentarios
Eduardo Orellana -
Palimp -
Gracias, y a seguir así.
Pedro -
Un saludo.
TioPetros -
Voy a ver qué es eso del mimetex, porque no sé ni de qué me estás hablando. Si no me entero, te lo preguntaré, vale?
mewt -
En otro orden de cosas, veo que intentas usar bastante notación matemática en tus posts. A lo mejor te interesaría instalar el plugin mimetex,
es un cgi que hay que copiar al directorio donde tengas este tipo de archivos, y traduce una versión reducida de codigo LaTeX a imagenes que no quedan mal del todo.
Yo lo puse en funcionamiento en 10 minutos y el resultado no es del todo malo, si te interesa y tienes alguna duda, no tienes más que avisar ;-)