Tamaños aparentes e ilusiones (2)
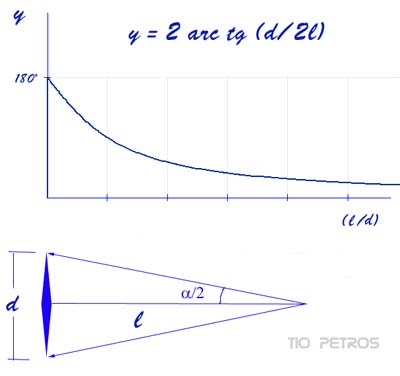 Todos sabemos que cuanto más lejos está un objeto, más pequeño lo vemos. Hablamos en todo caso de observación directa, sin instrumentos de aumento. Nos vendrá bien comprender el motivo y cuantificar un poco el asunto. En la figura aparece un objeto, como un rombo alargado, visto desde un punto a una distancia l, siendo d la diagonal mayor del rombo. Lo importante desde nuestro punto de observación es el ángulo alfa que ocupa el objeto. Cuando hablemos del tamaño aparente del rombo, nos referiremos a dicho ángulo. Con un poco de trigonometría, vemos que
Todos sabemos que cuanto más lejos está un objeto, más pequeño lo vemos. Hablamos en todo caso de observación directa, sin instrumentos de aumento. Nos vendrá bien comprender el motivo y cuantificar un poco el asunto. En la figura aparece un objeto, como un rombo alargado, visto desde un punto a una distancia l, siendo d la diagonal mayor del rombo. Lo importante desde nuestro punto de observación es el ángulo alfa que ocupa el objeto. Cuando hablemos del tamaño aparente del rombo, nos referiremos a dicho ángulo. Con un poco de trigonometría, vemos que tg (a/2)=d/(2·l)
y por lo tanto, a= 2 arc tg (d/(2·l))
Vemos por lo tanto que el tamaño aparente de un objeto depende exclusivamente de la relación (cociente) entre su diámetro real y la distancia que nos separa del mismo. Teneis la gráfica en la ilustración. Conviene recalcar que el eje horizontal no expresa distancias sino cociente de distancias, o si lo quereis: la distancia a la que estamos del objeto observado, tomando el diámetro del mismo como unidad de medida.
Es una función sin sorpresa alguna: decreciente y asintótica a cero, como debía ser. A distancia nula del objeto observado, su visión nos abarca 180 grados, lo que quiere decir que lo tenemos tan cerca que llena todo nuestro campo visual. Es lo que pasa con la tierra, que nos tapa exactamente la mitad del cielo si estamos en una zona completamente llana a ras de suelo.
El sol y la luna están aproximadamente a la misma distancia de nosotros si tomamos como escalas sus respectivos diámetros, de ahí que apreciemos aproximadamente el mismo tamaño en ambos. En ausencia de referencias añadidas, no tenemos evidencia directa de cuál de los dos está más cerca. Parecen dos astros de tamaño similar.
Sin embargo, resulta que el cerebro no se vale únicamente de los tamaños aparentes para estimar tamaños reales, sino que efectúa todo tipo de comparaciones. Pongamos un ejemplo: tengo en una calle a cierta distancia un niño con un globo, y tras él, bastante más lejos, otro niño con otro globo idéntico. Podemos hinchar el segundo globo hasta que desde mi punto de observación tenga el mismo tamaño aparente que el primero, pero en ese caso, no tendré ningún problema para saber que el globo más alejado es más grande: sé que está más lejos porque tengo mil referencias: ambos niños, la propia calle...) y lo aprecio moyor aunque tenga el mismo tamaño aparente que el cercano.
Eso es exactamente lo que pasa con el sol y la luna sobre el horizonte. Nuestro cerebro, por lo visto, imagina la bóveda celeste no como una semiesfera, sino como una cúpula elíptica, de forma que los puntos más alejados están en el horizonte, y el punto más cercano es el cenit. Aunque los tamaños aparentes son los mismos, una luna sobre el horizonte nos parece mayor porque la situamos más lejos que cuando está más alta.
Así de sencillo, sin necesidad de apelar a aberraciones atmosféricas, ni a cosas raras.
Y lo de las montañas que parecen alzarse sobre nosotros cuando nos alejamos en coche?
Si observan la gráfica de la curva de la ilustración, verán que la pendiente de la curva (su derivada, o ritmo de variación) va decreciendo paulatinamente (no podía ser de otra forma, si es asintótica a cero, continua y siempre positiva). Esto quiere decir que las variaciones de tamaño aparente según nos vamos acercando o alejando de los objetos que vemos serán mucho más acusadas para objetos que estén a distancias pequeñas de nosotros en (comparación con sus diámetros, no lo olvidemos !!!). Si nos alejamos de una montaña en coche, nos estamos alejando a una velocidad muy pequeña medida en (altura de montaña)/hora. Sin embargo, todo lo cercano que hace de marco a la montaña (los árboles que vamos dejando atrás, la propia carretera) sufre un efecto muy diferente: nuestra velocidad de separación medida en (altura de árbol)/hora es ahora muy grande a pesar de que nuestra velocidad real es la misma, y por lo tanto todo disminuye de tamaño a ritmo rápido menos la montaña, que lo hace muy lentamente. El efecto conjugado es que la montaña crece respecto al marco de referencia.
11 comentarios
MANUELA -
jony -
oniric -
Anónimo -
Naa, es fácil Dem, mira el termómetro...
Dem -
Es verdad, se reduce a la mitad como dices. Qué poca intuición matemática tengo XDDD (por eso me gusta esta página, aprendo cosas :D )
TioPetros -
Dem: Algo falla en lo que dices: explicas que separando el vaso al doble de distancia ha disminuido su tamaño aparente en menos de 1 cm. cuando los tamaños aparentes sólo podemos medirlos en grados...
Toma la gráfica, y verás que si doblas la distancia, el tamaño aparente se divide por dos. Un saludo.
JuanPablo -
Dem -
En la gráfica, a igual 'd', si doblamos 'l', 'y' no se reduce a la mitad. ¿'y' no indica el tamaño aparente del objeto?
No me refiero a la montaña en comparación a un árbol sino a cualquier objeto aislado. Por ejemplo, acabo de coger un vaso y medido su altura aparente. Lo he desplazado al doble de distancia (25 cm) y su altura aparente se ha reducido en menos de un cm. (Dem metido a científico, jeje, tiembla mundo).
Pensándolo bien, no se si el concepto de "tamaño aparente" lo he captado bien. Para el "experimento" del vaso, he usado una regla en vertical sobre la mesa y a 10 cm de mi cara para medir la "altura aparente" del vaso.
TioPetros -
No creo que sea demostrable el asunto de la cúpula celeste. Por lo que he leído del asunto, es una teoría de la percepción humana que explica el efecto del agrandamiento del sol y de la luna sobre el horizonte, pero de ahí a demostrarlo...
Dem -
En cuanto a eso de que nuestro cerebro concibe la esfera celeste como una cúpula elíptica... me parece más raro. ¿Eso es demostrable? No digo que lo demuestres, sólo que si es posible hacerlo (haría un acto de fe y me lo creería ;P )
dob -
Supongo que es cuestión de perspectiva y de relación diámetro/distancia, igual que las montañas.