Maraña de rectángulos ( y 2)
 Como se ha afirmado en los comentarios del post anterior, debemos buscar la disposición de rectángulos que haga máximo el número de subdivisiones del plano, y esa disposición es la que tenga mayor número de intersecciones entre los rectángulos.
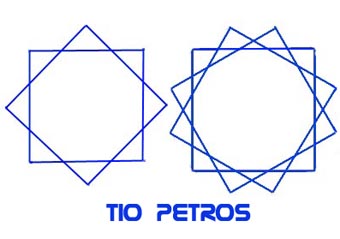
Como se ha afirmado en los comentarios del post anterior, debemos buscar la disposición de rectángulos que haga máximo el número de subdivisiones del plano, y esa disposición es la que tenga mayor número de intersecciones entre los rectángulos.Dados dos rectángulos, el número máximo de intersacciones es de ocho, y se da cuando están girados uno respecto de otro. La situación se observa perfectamente considerando cuadrados (rectángulos al fin y al cabo) concéntricos y girados 45 grados uno respecto al otro. Definen nueve regiones. Ocho regiones que pertenecen tan sólo a un rectángulo (las puntas) y otra grande que pertenece a ambos.
Cuando tenemos tres rectángulos tenemos 4·3=12 puntas que pertenecen a un solo rectángulo, otras doce que pertenecen a dos y una que pertenece a los tres. (ver figura)
En el caso general, tenemos 4n regiones que pertenecen a un sólo rectángulo (las puntas), y el mismo número de regiones que pertenecen a dos, a tres... a (n-1) rectángulos y una sola que pertenece a todos ellos.
Compruébenlo en la ilustración siguiente, para el caso de cinco cuadrados:

Por tanto, operando un poco, si llamamos F(n) al número de regiones en que se divide el plano con n rectángulos en esta disposición, tenemos:
F(n) = 1 + 4n + 4n + ... +4n donde hay (n-1) sumandos de 4n.
Por tanto:
F(n) = 1 + 4n(n-1)=1 + 4n2 - 4n = (2n-1)2
Dado que teníamos F(n)= 18.769 regiones, el número mínimo de rectángulos corresponderá con el número de rectángulos de la disposición anterior, de máxima intersección. Tenemos:
18.769 = (2n-1)2
Osea, n = 69; como había afirmado none en un comentario anterior, y no 68 como había dicho yo...
Así pues, podemos afirmar que el número de rectángulos de la disposición del enunciado tiene en 69 su cota mínima.
PD.- Mewt planteaba en los comentarios la ecuación F(n)=2 + 4n(n-1), seguramente contando la región no acotada exterior a todos los rectángulos. En el enunciado se eliminaba la contabilización de la zona no acotada para evitar dudas.
1 comentario
Generic Cialis -