Blogia
Tio Petros

Triángulos sobre una cuadrícula

- Para pensar
Triángulos sobre una cuadrícula Hace cierto tiempo hablábamos del teorema de Pick, y comentábamos que sobre una simple cuadrícula se pueden hacer muchas matemáticas. Hoy me encontrado con un teorema sencillo, a modo de divertimento, que les propongo.
Se trata de ver si puede existir un triángulo equilátero cuyos vértices estén sobre los puntos de una cuadrícula dada. Así de escueto.
Les espero.

24 comentarios

rodrigo -

al ver que no ponen nada importante no sirve esta pagina no sigan perdiendo su tiempo en este sitio de internet

octavio herrera hernandez -

el america no sirve arriva el cruz azul le vamos a ganar al chivas

valteram -

El área triangulo (y en general de un polígono) con vértices en los puntos de una cuadrícula entera es igual a: I+1/2*B-1, donde I es el número de puntos(de la cuadrícula) interiores al polígono y B los puntos en los bordes. Esta fórmula es el teorema de Pick. Como consecuencia de esta fórmula se deduce que los polígonos con vértices en una cuadrícula entera tienen Áreas que son números racionales (dado que I y B son enteros). Por lo tanto si existe un triángulo equilátero con vértices en los puntos de la cuadrícula, su área debe ser un número racional. Tenemos además que el área de un triángulo equilátero es el producto entre base y altura: b*h, y puesto que h=b*raiz(3)/2, tenemos que Área= raiz(3)*b^2/2. Ahora como b^2 es racional, puesto que es el área de un cuadrado de lado b con vértices en la cuadrícula, entonces obtenemos que raiz(3) es racional, lo cual sabemos que no es cierto. Entonces queda demostrado que no existe un Triángulo equilátero con sus vértices en los puntos una cuadrícula.

princess -

porfa alguien ayudeme necesito que son las coordenadas, en que se clasifican y que es cada una de sus clasificaciones en el plano

lamaphia_frik -

tras varios intentos descubri que hay un modo en el que podemos representar el triangulo equilatero de manera que los vertices tengas coordenadas enteras (refiriendome a coordenadas enteras como numeros enteros) lo demostraremos asi:
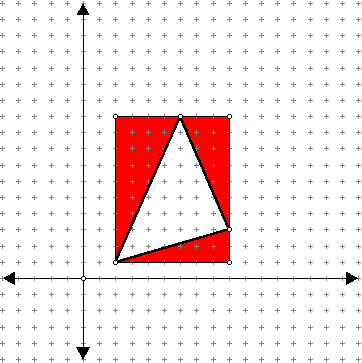
si colocamos el triangulo en medio de los 4 cuadrantes que contiene un plano cartesiano como el que se nos muestra en la figura podemos demostrar esto tomando de referencia los siguientes puntos (-x,0),(x,0), (0,y). supongamos que x=3 como -x=-3 y y=5 entonces posicionandonos en el plano (preferentemente hacer el dibujo) podemos darnos cuenta deque se forma un triangulo equilatero y ademas con numeros entero de este modo podriamos decir que tenemos la respuesta dependiendo de a que se refiera la pregunta.

ahora el problema siguiente es si la pregunta se refiere a poner un triangulo equilatero tal cual que x=y=-x entonces se comprueba que no es posible dibujar un triangulo equilatero de esta manera dado que lo alto, en este caso y, del triangulo siempre quedaria en coordenadas diferentes a las de x.

david -

esto es una barsofia

cony -

a la wea cabezona ujaujujauja kmo pueden ¬¬ .. ujajujaa pero bien por ustedes es bueno k aya gente tan observadora en este mundo
aios

flaca -

no les entiendo

oniric -

coordenadas: estoy en una cuadrícula con cuadrados de 5mm. de lado; el equilátero en teoría es de 5cm.*5*5. La altura es de 4,5 cm. Por tanto, aplicando el teorema de >Pitágoras....no es un triángulo equilátero, a pesar de que lo parecía, midiéndolo deprisa con la regla.
Va a ser que Pitágoras estaba equivocado :P
Y dicho esto, me retiro prudentemente...

mewt -

oniric: Puedes darnos las coordenadas de los vertices? Estoy seguro de que tu triangulo no es en realidad equilatero...

Nico: Nada hombre, no te preocupes, para tener una idea nueva y buena tienes que tener 100 malas antes...

oniric -

Mewt, pues yo lo tengo; un equilátero de 5*5*5 ¿¿¿¿????

Duende: Kepler, que era un poco torpe, hacía matemáticas y física de ese modo.

Pero, vamos, que yo no puedo discutir mucho, que no tengo ni idea; dejé las mates hace mucho, por prescripción facultativa.
Un saludo: Oniric

Nico -

mewt, mi razonamiento iba completamente equivocado y apresurado. Gracias por la rectificacion.

Duende: lo mismo.

:_(

Duende -

pepe y mewt, cierto. Gran cagada :-) Va otra vez:

Si asumimos que uno de los lados está entre dos vértices que distan a cuadrículas horizontalmente y b cuadrículas verticalmente, el vértice opuesto estará en la siguiente posición respecto al primero de los vértices:

x = a/2 + b*raíz(3)/2 (ó x = a/2 - b*raíz(3)/2)
y = b/2 + a*raíz(3)/2 (ó y = b/2 - a*raíz(3)/2)

No existen a y b enteros distintos de cero que hagan que x e y sean enteros, luego el vértice no está en un punto de la cuadrícula.

Eligiendo a y b determinamos un lado, que determina dos posibles triángulos equiláteros -> de este modo no es posible insertar un triángulo equilátero en la cuadrícula.

A ver si esta vez es la definitiva :-)

Saludos,
Duende

mewt -

Estoy de acuerdo con pepe, yo tambien pensaba que la demostracion que tenias es la que ha dado el (que, por cierto, tambien demuestra la imposibilidad de dibujar un poligono reticular regular de cualquier numero de lados distinto de 4 y 8).
La mia, aunque a ti te parezca complicada, es muy natural cuando uno piensa en la cuadricula como en su grupo de simetrias, e interpreta el dibujar el poligono dentro como encontrar un subgrupo determinado dentro de el grupo grande. Maneras diferentes de ver las cosas, supongo...

pepe -

Lo siento Duende, pero no puedo estar de acuerdo, estás dando por supuesto que uno de los lados es una de las líneas de la cuadrícula, y no tiene por que ser así, de modo que no necesariamente hay un lado de longitud n entero, si la diferencia entre las coordenadas x es n, y entre las y es m, la longitud del lado es raiz(n²+m²), de modo que de ese modo ya introducimos radicales, y podría aparecer (sin mirar las cosas más detenidamente) otro vértice con diferencias entre sus coordenadas a y b tales que raiz(a²+b²)=raiz(n²+m²), pero lo que esta prohibido es que el ángulo entre ambos sea de 60 grados, por lo que acabo de poner como demostración, que, por cierto, tampoco creo que sea tan complicada.

Duende -

mewt: joer, no te has complicado la vida ni ná con la primera de tus opciones XD. Supongo que lo que pretendías era generalizarlo para el caso de otros polígonos. Por otro lado, desde luego que si escogemos retículas inclinadas o rectangulares no cuadradas sería posible.

Nico: raíz de tres

Oniric: no se trata de buscar triángulos como quien busca minerales :-) En general las Matemáticas tienden más a teoremas y apriorismos y no a hallazgos fortuitos y experimentales. La demostración cuasi-completa la tienes arriba. Aún así, quedaría demostrar por qué n*raíz(3)/2 no puede ser entero siendo n real.

pepe: a tu demostración la incluímos dentro del sadomasoquismo matemático XD

Saludos,
Duende

Duende -

Venga, ¡va!, lo voy a demostrar.

Imaginemos un triángulo equilátero con uno de sus lados en horizontal (la base), y por sencillez, imaginemos que el vértice opuesto está por encima d ese lado.

Supongamos que los vértices del triángulo están en dos puntos de la cuadrícula, distantes en n unidades de cuadrícula entre sí. Obviamente, n debería ser par para que el otro vértice estuviera situado en una línea vertical de la cuadrícula. Para que estuviera situado en una línea horizontal de la cuadrícula se debería cumplir que la altura del triángulo (distancia desde la base y el vértice superior) equivale a un número entero de unidades de cuadrícula. Esto es imposible porque la altura sería n*raíz(3)/2 (esto se obtiene por trigonometría o por Pitágoras), y este número no es entero (en esto último alguno quizás tenga que hacer acto de fe).

¿Por qué es n*raíz(3)/2? Usamos Pitágoras: dividimos el triángulo expuesto en dos partes, izquierda y derecha, y nos quedamos con la izquierda. Nos queda un triángulo rectángulo cuya hipotenusa tiene n como longitud. El lado pequeño de abajo valdría n/2. El lado que falta (la altura) la obtendríamos así: a^2 = b^2+c^2 -> n^2 = b^2+(n/2)^2 -> (3/4)*n^2 = b^2 -> raíz(3/4)*n = b -> b = raíz(3)*n/2 (l.q.q.d. = lo que queríamos demostrar)

Saludos,
Duende

pepe -

Supongo que la demostración a la que alude Duende será más o menos la siguiente:
Supongamos que en el lado inferior la diferencia de las coordenadas y es m (entero) y la diferencia de las x es n (también entero), entonces la tangente del ángulo que forma con el eje X es m/n (racional), supongamos que el ángulo es A=arctan(m/n).
Consideremos ahora el lado de la izquierda, el ángulo que forma con el eje X es de A+60º, luego:
tg(A+90)=(tg(A)+tg(90))/(1-tg(A)tg(90))
pero estamos suponiendo que el vertice superior también tiene coordenadas enteras, y por tanto tg(A+60º)=a/b, también racional, igualando ambas expresiones se obtiene, llamando r(3) a la raiz de 3:
a/b=(m/n+r(3))/(1-r(3)m/n)
y quitando los denominadores queda:
r(3)(nb+ma)=na-mb
y si nb+ma es distinto de 0, obtenemos que raiz de 3 es racional, lo cual es falso, y si nb+ma=0, debería ser también na-mb=0, y entre las dos ecuaciones obtenemos un sistema lineal homogeneo con 2 ecuaciones y dos incógnitas (a y b), y cuyo determinante es n²+m², que no puede ser 0, luego la única solución es a=0, b=0, es decir el único punto de vértices enteros del segundo lado es precisamente el dado. Y por tanto no hay solución.

mewt -

Anonimo: Ein? Justamente si exiges que uno de los lados del triangulo este en la cuadricula es obvio probar que no se puede, ya que en ese caso la longitud del lado es un entero (suponiendo que la cuadricula es 1x1) y la longitud de la altura tambien tendria que ser un entero, y sabemos que en un triangulo equilatero la altura es Raiz(3)/2 veces la longitud del lado, que jamas puede ser entero, ni siquiera racional, siendolo la longitud del lado.

nico: No se por donde ira tu razonamiento, en el que se me ocurre a mi es raiz de 3 el numero que aparece...

Anónimo -

Hola. Si se admite que uno de los lados coincida con una linea de la cuadrícula, va a ser que sí. Pero imagino que no se admite, por que en ese caso yo habría encontrado un equilátero difícil de hallar en medio segundo, y eso sí que es imposible.
De todas formas, sé que el hecho de que no se pueda encontrar fácilmente no significa que no esté, a menos que se establezca el teorema.
Imagino que por ahí va el razonamiento de Duende.
Saludos,
Oniric

Nico -

La raiz de tres o la de cinco?

mewt -

Si la reticula es cuadrada, efectivamente la respuesta es no. Un argumento con el que se puede demostrar es similar al que ya mencionaba en el comentario del post del Teorema de Pick cuando decia que un pentagono regular no se puede ver como poligono reticular para ninguna reticula. Lo dejo aqui por si alguien no quiere que le estropee el misterio, si pasado un tiempo prudencial no hay solucion detallada, y a alguien le interesa, lo mismo me animo y la redacto ;-)
Hay otro argumento mas trigonometrico, y probablemente mas corto, que me imagino que es en el que piensa Duende, con el que se establece la imposibilidad de formar no ya un triangulo equilatero, sino un angulo de 60 grados dentro de una cuadricula (lo cual, en particular, implica lo del triangulo).

Por supuesto, en algunas reticulas no cuadradas si que es posible colocar el triangulo equilatero: piensese por ejemplo en la reticula generada por dos vectores unitarios que formen entre si un angulo de 60 grados.

Duende -

No, no se puede. Esencialmente porque la raíz cuadrada de tres no es un número racional (es decir, derivado de la razón de dos números enteros. Esto se podría demostrar más detalladamente. Saludos.

Anabel -

Tras un momento de sorpresa, pensando que no hay ningún motivo por el cual no pueda existir tal triángulo, me pongo a hacer unos dibujos... y resulta que no consigo ningún triángulo equilátero sobre una cuadrícula. Estoy empezando a pensar que la respuesta es NO, pero no lo sé demostrar...