Contando sudokus
Habrán pensado que este blog ha dejado de actualizarse...
En realidad ocurren dos cosas; una es la falta de pericia de su autor para seguir proponiendo paseos matemáticos, que pasados dos años de actividad regular se va resintiendo, y otra es el periodo veraniego, poco apto para estas cosas. Sabrán perdonarme por ambas cuestiones.
Para paliar un poco este silencio les propongo un reto difícil. Calcular el número de SUDOKUS lícitos.
Como supongo que sabrán, un sudoku es un cuadrado de 9x9 casillas (puede ser de otro tamaño, pero consideraremos este, por ser el más habitual. Las casillas están agrupadas en nueve subcuadrados de 3x3. Pues bien; se deben rellenar las casillas con números del 1 al 9 de manera que no se repitan ni en las filas, ni en las columnas ni en los subcuadrados de 3x3.
Aquí tienen una explicación algo más pormenorizada de lo que es un sudoku, en el hipotético y extraño caso de que no se lo hayan encontrado aún en la sección de pasatiempos de cualquier periódico.
Ya hemos dicho varias veces que la combinatoria, no siendo más (ni menos) que el arte o la técnica de contar elementos de conjuntos), puede ser una disciplina apasionante y muy complicada. Aquí tienen un ejemplo.
Les espero.
En realidad ocurren dos cosas; una es la falta de pericia de su autor para seguir proponiendo paseos matemáticos, que pasados dos años de actividad regular se va resintiendo, y otra es el periodo veraniego, poco apto para estas cosas. Sabrán perdonarme por ambas cuestiones.
Para paliar un poco este silencio les propongo un reto difícil. Calcular el número de SUDOKUS lícitos.
Como supongo que sabrán, un sudoku es un cuadrado de 9x9 casillas (puede ser de otro tamaño, pero consideraremos este, por ser el más habitual. Las casillas están agrupadas en nueve subcuadrados de 3x3. Pues bien; se deben rellenar las casillas con números del 1 al 9 de manera que no se repitan ni en las filas, ni en las columnas ni en los subcuadrados de 3x3.
Aquí tienen una explicación algo más pormenorizada de lo que es un sudoku, en el hipotético y extraño caso de que no se lo hayan encontrado aún en la sección de pasatiempos de cualquier periódico.
Ya hemos dicho varias veces que la combinatoria, no siendo más (ni menos) que el arte o la técnica de contar elementos de conjuntos), puede ser una disciplina apasionante y muy complicada. Aquí tienen un ejemplo.
Les espero.
 A un congreso sobre creacionismo científico asisten 1.400 personas.
A un congreso sobre creacionismo científico asisten 1.400 personas.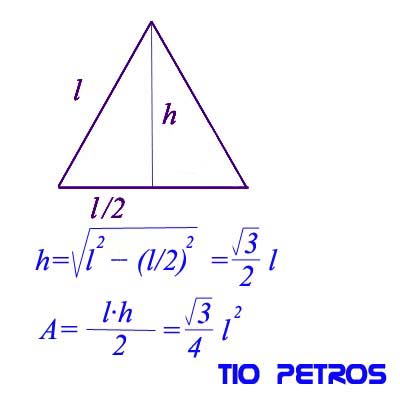 Vamos a exponer una de las posibles demostraciones de que es imposible dibujar un triángulo equilátero con vertices en los puntos de una cuadrícula, como exponíamos en el post anterior. Como bien ha sido expuesto en los comentarios de ese post, la cuadrícula se supone ortogonal. Cada lado de la cuadrícula elemental se toma como unidad de medida.
Vamos a exponer una de las posibles demostraciones de que es imposible dibujar un triángulo equilátero con vertices en los puntos de una cuadrícula, como exponíamos en el post anterior. Como bien ha sido expuesto en los comentarios de ese post, la cuadrícula se supone ortogonal. Cada lado de la cuadrícula elemental se toma como unidad de medida.
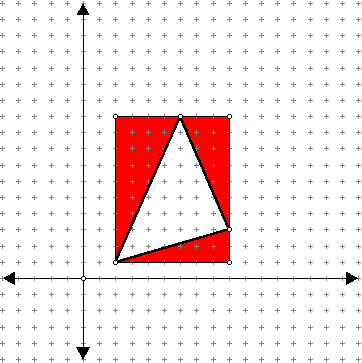 Hace cierto tiempo hablábamos del teorema de Pick, y comentábamos que sobre una simple cuadrícula se pueden hacer muchas matemáticas. Hoy me encontrado con un teorema sencillo, a modo de divertimento, que les propongo.
Hace cierto tiempo hablábamos del teorema de Pick, y comentábamos que sobre una simple cuadrícula se pueden hacer muchas matemáticas. Hoy me encontrado con un teorema sencillo, a modo de divertimento, que les propongo. Hemos hecho hincapié varias veces en el blog de la importancia de la experimentación en la validación de las teorías científicas. Si la ciencia es el estudio de lo real, es lo real quien debe refrendar la utilidad si no la verdad de nuestra teoría.
Hemos hecho hincapié varias veces en el blog de la importancia de la experimentación en la validación de las teorías científicas. Si la ciencia es el estudio de lo real, es lo real quien debe refrendar la utilidad si no la verdad de nuestra teoría. 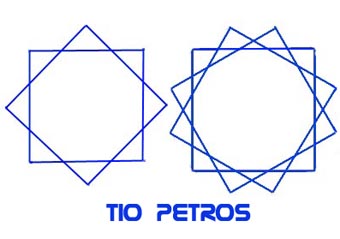 Como se ha afirmado en los comentarios del post anterior, debemos buscar la disposición de rectángulos que haga máximo el número de subdivisiones del plano, y esa disposición es la que tenga mayor número de intersecciones entre los rectángulos.
Como se ha afirmado en los comentarios del post anterior, debemos buscar la disposición de rectángulos que haga máximo el número de subdivisiones del plano, y esa disposición es la que tenga mayor número de intersecciones entre los rectángulos.
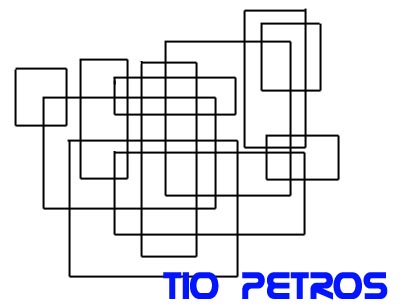 Les propongo un problema que acabo de encontrar:
Les propongo un problema que acabo de encontrar: La teoría de superficies es una de las partes más bellas por lo visual de la matemática.
La teoría de superficies es una de las partes más bellas por lo visual de la matemática.
 Había una vez un monasterio en el que vivían un grupo de cincuenta monjes. Todos ellos eran especialistas en lógica matemática y tenían voto de silencio. Pero el voto era muy estricto: no sólo no podían hablar entre sí; tampoco podían intercambiar mensajes por procedimiento alguno. Ni por escrito, ni por señas, ni nada. Además, como sólo cultivaban el espítiru, tampoco tenían espejos ni manera de contemplarse a sí mismos. Sólo hacían una comida al día, en el refectorio común, todos a la vez en una enorme mesa redonda, y el resto del día lo pasaban orando y estudiando lógica en sus celdas.
Había una vez un monasterio en el que vivían un grupo de cincuenta monjes. Todos ellos eran especialistas en lógica matemática y tenían voto de silencio. Pero el voto era muy estricto: no sólo no podían hablar entre sí; tampoco podían intercambiar mensajes por procedimiento alguno. Ni por escrito, ni por señas, ni nada. Además, como sólo cultivaban el espítiru, tampoco tenían espejos ni manera de contemplarse a sí mismos. Sólo hacían una comida al día, en el refectorio común, todos a la vez en una enorme mesa redonda, y el resto del día lo pasaban orando y estudiando lógica en sus celdas. Hemos dicho varias veces en este blog que las verdaderas paradojas no existen. Es gratificante pensar que siempre debe existir una explicación de porqué un aparentemente correcto razonamiento nos lleva a dos conclusiones contradictorias. Y es gratificante porque en caso contrario, existe un teorema que afirma que si en un sistema axiomático pueden ser demostradas dos proposiciones contradictorias, entonces puede ser demostrada cualquier afirmación. Lo cual es lo mismo que decir que el sistema no vale un pimiento.
Hemos dicho varias veces en este blog que las verdaderas paradojas no existen. Es gratificante pensar que siempre debe existir una explicación de porqué un aparentemente correcto razonamiento nos lleva a dos conclusiones contradictorias. Y es gratificante porque en caso contrario, existe un teorema que afirma que si en un sistema axiomático pueden ser demostradas dos proposiciones contradictorias, entonces puede ser demostrada cualquier afirmación. Lo cual es lo mismo que decir que el sistema no vale un pimiento. A estas alturas de la vida uno no ve posible (ni seguramente deseable) que la España entera llore la muerte de los grandes hombres que a cuentagotas nos van dejando para siempre. Cada uno tiene los suyos; yo desde esta bitácora desearía resaltar a
A estas alturas de la vida uno no ve posible (ni seguramente deseable) que la España entera llore la muerte de los grandes hombres que a cuentagotas nos van dejando para siempre. Cada uno tiene los suyos; yo desde esta bitácora desearía resaltar a