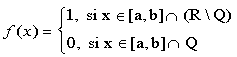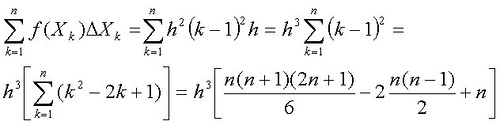Prolegómenos a la integral de Lebesgue

Viene de aquí. 

Vistos los problemas que tenemos con ciertas funciones, relativamente sencillas de definir y de muy mal comportamiento, la estrategia de Lebesgue es bien diferente de la estrategia de Riemann.

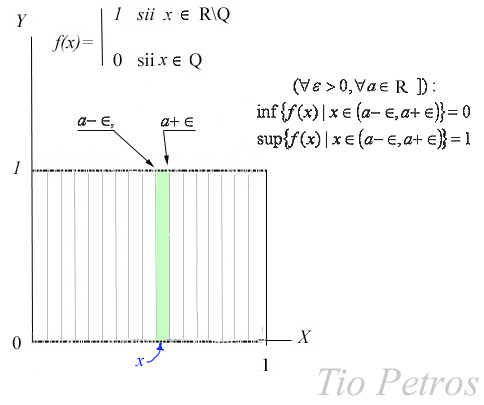
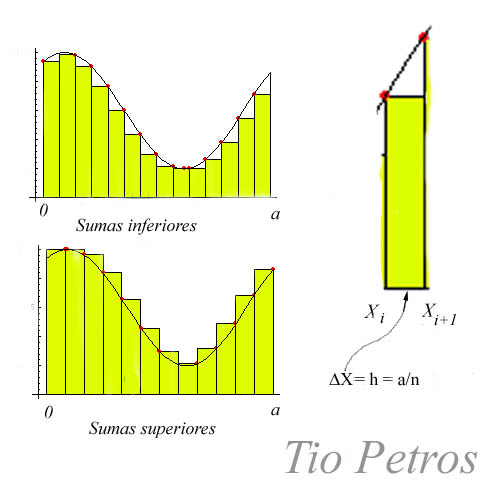
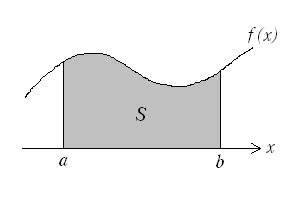
Cuando integramos en el sentido de Riemann, definimos una operación de conteo en gran medida de forma independiente de los valores que adopta la función, y así pasa lo que hemos visto con funciones como la de Dirichlet. Las sumas que aproximan la integral de Riemann provienen de partir el intervalo de integración en particiones sucesivamente más finas, y aproximar el área bajo la gráfica por exceso y por defecto mediante rectángulos, como hemos visto hace dos posts. Si tenemos una función de buen comportamiento , la diferencia entre las medidas por exceso y por defecto tenderán a cero cuando aumentamos la finura de la partición, en cuyo caso la función es Riemann-integrable.

Es importante comprender que en este método las particiones se realizan de forma independiente de los valores de la función.

Lebesgue, intentando extrapolar el concepto de integral a todas la funciones construibles, partió de un punto totalmente diferente. Fijándose precisamente en qué trozos del intervalo de integración la función tomaba ciertos valores.

Dado que en la generalidad más absoluta tendremos funciones que varíen continuamente, se trataba de aproximar cualquier función mediante lo que se llamaron funciones simples. Así pues, al definir la integral de Lebesgue la propia función es la que determinará los conjuntos sobre los que se definen las funciones simples que sirven para definir la función que queremos integrar. Es un proceso constructivo que se puede aplicar a toda función constructiva, y que requiere una cierta tranquilidad para ser visto convenientemente, por lo que lo haremos sin prisas, deteniéndonos donde sea necesario.

El proceso que seguiremos será más o menos el siguiente:

1.- Definiremos qué es una función medible en un espacio de medida.

2.- Definiremos qué es una función simple, y veremos que es un tipo de funciones medibles.

3.- Definiremos la integra de Lebesgue de funciones simples.

4.- Veremos cómo cualquier función medible se puede expresar como llímite de una función simple, y definiremos la integral de Lebesgue de funciones simples.

Será entonces cuando, en virtud de las buenas propiedades en el límite de esta integral, podremos extrapolar el concepto de integral de Lebesgue a toda función medible, construible mediante el paso al límite de funciones simples.

Nos llevaremos la sorpresa de que una función diabólica como la de Dirichlet cae en el paso tres, sin siquiera necesidad de pasos al límite.

De momento, ese es el guión; pero vaya por delante un comentario coloquial sobre la diferencia de las integraciones en el sentido de Riemann y de Legesgue que encontré en un libro sobre el tema:

Sobre una mesa hay esparcidas una serie de monedas. Para contar la cantidad de dinero que hay sobre la mesa Riemann dividiría la misma en una serie de bandas, calculando el dinero que cae dentro de cada banda para sumar después. Lebesgue sin embargo agruparía las monedas de valores iguales en montones, calcularía fácilmente el valor de cada montón y luego sumaría los montones.

Volveremos a este símil una vez explicado todo el asunto.

En la imagen que encabeza el post, tienen a Henry León Lebesgue (1875-1941) , matemático francés que dió su nombre (entre otras cosas) a esta nueva manera de entender la integración.

La función de Dirichlet

Viene de aquí. 

Trataremos en este post de ver cómo existen situaciones relativamente sencillas para las cuales la integral de Riemann no es aplicable.

Adelantamos que en ciertas situaciones aparecen funciones que no son riemann-integrables, y pusimos como ejemplo un problema de cálculo de probabilidades:

¿Cuál es la probabilidad de que eligiendo un punto del intervalo [0,1] al azar el punto elegido sea irracional?

Sea una función real de variable real definida en el intervalo [0,1], de la manera siguiente:

Esta función recibe el nombre de función de Dirichlet.

La función vale la unidad para todo punto de [0,1] irracional, y cero para todo punto racional de dicho intervalo. Por lo tanto, la función está definida para todo punto de [0,1].

La representación gráfica de esta función es un poco difícil: entre dos puntos racionales cualesquiera de [0,1] hay infinitos puntos irracionales, y la recíproca también es cierta, así que la gráfica de la función consta de una nube lineal de puntos de ordenada unidad y otra nube lineal de puntos de ordenada nula.

Cuál es el valor esperado de dicho experimento? Un uno es que hemos obtenido un irracional y un cero lo contrario. Cuando hablamos de la insoportable levedad del conjunto Q explicamos que a pesar de la aparente reciprocidad entre Q y R-Q (entre dos irracionales siempre hay infinitos racionales y viceversa), ambos tenían propiedades cardinales muy diferentes: Q es numerable y R-Q tiene la potencia del continuo. Los irracionales contenidos en [0,1] forman un conjunto incomparablemente mayor que los racionales, y esto nos legitima "de alguna manera" a concluir que la probabilidad de que resulte elegido un racional es nula.

Este "de alguna manera" es una vaga invocación a la ley de Laplace de casos favorables entre casos posibles, si bien entre dos conjuntos infinitos la cosa deja mucho de estar clara aunque la intuición resulta (esta vez) ser correcta.

Veamos que la integral de Riemann no nos sirve de gran ayuda en este aspecto. Intentemos integrar la función de Dirichlet por medio de las sumas superiores e inferiores definidas en el post anterior.

A poco que pensemos, vemos que en cualquier elemento de una partición del intervalo [0,1], por muy fina que sea habrá dos clases de puntos: los que tienen la función igual a uno y los que la tienen igual a cero.

Por lo tanto las sumas superiores suman la unidad, mientras que las inferiores son una suma de sumandos nulos, que es nula. No hay por tanto convergencia de las I(f,P) con las S(f,P) del post anterior.

Tenemos que I(f,P)=0 y S(f,P)=1 para cualquier partición P. Por ello I^*(f) = 1 ≠ 0 = I_*(f) y por lo tanto la función no es Riemann integrable. Como intuimos, la solución a este inconveniente vendrá desde la teoría de la medida...

La integral de Riemann

Viene de aquí . 

La integral de Riemann está basada en la llamada Medida de Jordan, y se expresa como el límite de una suma de Riemann. Vayamos por partes para entender esto.

El concepto de medida en matemáticas generaliza los conceptos habituales de longitud, área y volumen; y trata de conseguir que clases cada vez más generales de conjuntos tengan asociada una medida. Dichos conjuntos se llamarán conjuntos medibles.

Nos limitaremos al cálculo de áreas de figuras planas, si bien la extrapolación a dimensiones superiores no aporta dificultad conceptual alguna, sino merametne operativa.

La idea de la medida de Jordan consiste en atrapar la figura a medir en enlosados de rectángulos (el valor de las áreas de estos últimos son fáciles de hallar). Cuanto más fino sea el enlosado más fielmente se adaptará alas posibles anfractuosidades de la figura, de forma que es esperable que el límite del enlosado sea exactamente la medida de la figura.

A modo de test, para que dicho límite sea unívocamente determinado, se efectuarán enlosados exteriores e interiores. Los primeros cubren el conjunto de partida, y los segundos son cubiertos por él. Si el límite de las áreas por enlosados exteriores e interiores son iguales, entonces decimos que la figura es medible- Jordan, y que su medida es el valor de dichos límites coincidentes. Las sumas de los rectángulos interiores las llamaremos sumas inferiores de Riemann, y las de los extreriores sumas superiores de Riemann. Para cualquier tipo de división finita en rectángulos, la suma inferior será menor que la superior, de ahí la nomenclatura.

Es comprensible esperar que en el límite, cuando el número de rectángulos tienda a infinito porque la partición realizada en en intervalo de integración sea extremadamente fino, tanto la suma inferior como la exterior se acercarán, una por arriba y otra por abajo a la cantidad buscada. Esa es al menos la esperanza, y las funciones que así lo cumplen serán denominadas funciones Riemann-integrables.

En la mayor parte de las matemáticas que se necesitan en la física y en la ingeniería este sistema de integral es suficiente porque las figuras a tratar (planas o no) son medibles en el sentido de Jordan.

Podemos ver la idea en la siguiente imagen:

Veamos detenidamente el proceso con el cálculo de la medida bajo una parábola.

Sea la parábola f(x) = x² .

Una partición P del intervalo cerrado [a, b] es un conjunto finito de puntos P = { x₁, x₁, x₂, ..., x_n+1} tal que:

a = x₁ < x₂ < x₃ < ... < x_n < x_n+1 = b

El proceso comienza efectuando una partición de este tipo.

Fijémonos en los rectángulos interiores de la figura.

La base de todos ellos mide ΔX = a/n, cantidad que llamaremos h.

Comenzaremos hallando la La suma inferiores de f respecto de la partición P

Las alturas son función de la gráfica que queremos integrar. Dado que los estamos preocupando de los rectángulos interiores las alturas serán las correspondientes al valor más pequeño de la función entre ambos extremos (en realidad estamos interesados en el ínfimo de la función en el intervalo. En nuestro caso, y dado que la función es creciente en el intervalo considerado, el extremo a considerar será el izquierdo.

Debemos hallar los siguientes valores:

f(X₁)=f(0)=0

f(x₂) = f(ΔX) = f(h) = h²

f(x₃) = f(2ΔX) = f(2h) = (2h)²

y por inducción:

f(x_k) = f[(k-1)ΔX] = [[(k-1)h]² = h²(k-1)²

Ahora no tenemos más que sumar las áreas de todos los rectángulos, quedando algo como esto:

A este valor lo llamaremos suma inferior de Riemann para la función f y la partición P, I(f,p).

Ahora no tenemos más que tomar límites cuando n tiende a infinito, obteniendo el valor de la integral inferior de Riemann I_*(f).

La integral inferior de Riemann no depende de la partición considerada por ser el límite cuando ésta es infinitametne fina.

Fácilmente teniendo en cuenta que h=a/n, obtenemos:

No lo haremos aquí, pero si repetimos el mismo cálculo para las suma superiores de f respecto de la partición P , que denotaremos S(f,P) y volvemos a calcular límites, obtendremos el valor I^*(f), integral superior de Riemann para la función f. Obtendríamos igualmente el valor de a³/3, lo que indica que las áreas limitadas con las sumas inferiores y superiores convergen a un mismo valor, que es la llamada integral de Riemann de la función en el intervalo considerado.

Así pues, la condición de integrabilidad en el sentido de Riemann es que se de la igualdad I_^*(f) = I_*(f)

¿Cómo serán las funciones que no cumplan esto último? Mostrar que las funciónes no Riemann-integrables aparecen incluso en sencillos problemas de probabilidad es el propósitop del próximo post. Una vez detectada la insuficiencia de la integral de Riemann, tenemos el camino abierto para generalizar el concepto y encontrar una herramienta que coincida con la de Riemann en las funciones Riemann-integrables, y que además sea válida para un mayor número de funciones.

La solución vendrá de la mano del francés Henry Lebesgue y será válida para todas las funciones que se puedan definir de manera constructiva.

Pero no adelantemos acontecimientos.

De la esperanza a la integral de Lebesgue

No es que de la definición de esperanza de una variable aleatoria lleguemos al concepto de integral de Lebesgue, sino que nos apoyamos en el concepto de esperanza matemática que hemos visto varias veces en el blog, y lo utilizamos como escusa para explicar un concepto de integral que supera al tradicional de Riemann.

Hemos definido varias veces la esperanza de una variable aleatoria como la suma de los productos de los posibles valores de la misma por las probabilidades de que adopten esos valores.

Si X es una V.A. que puede tomar valores x₁,...,x_n con probabilidades p₁,..,p_n, (p₁+...+p_n = 1 ) entonces la esperanza de la variable X es:

E[X] = x₁p₁ + ... + x_np_n

Cuando la variable es continua y toma valores en un intervalo [a,b], no podemos hablar de probabilidad de que tome un valor concreto, pues en el caso genérico, cada valor concreto tiene probabilidad nula de ocurrir (son infinitos los posibles). Hablaremos de densidad de probabilidad, entendiendo la densidad de probabilidad de un punto como el límite del cociente entre la probabilidad de un segmento que contenga a dicho punto y la longitud de dicho segmento, cuando ésta tiende a cero.

El operador esperanza se ha convertido en una integral . Sin embargo tenemos un problema: la integral habitual que se usa en ingeniería es la integral de Riemann, y se muestra absolutamente incapaz de hacer frente a problemas probabilísticos, incluso a algunos muy sencillos, como el siguiente:

¿Si escogemos un número en el intervalo [0,1] al azar cuál es la probabilidad de que el número escogido sea irracional?

La solución a este problema, casi trivial, muestra que la integral de Riemann es incapaz de afrontar contajes (pues una integral no es sino una forma de contar) en espacios abstractos como los espacios probabilísticos. Por ello hace falta una herramienta conceptual más elaborada que vendrá de la mano de Lebesgue.

Todo ello lo veremos en los próximos días. Daremos un repaso al concepto de Integral de Riemann, y veremos porqué en los casos más generales no es satisfactoria.

Hablar de integrales es hablar de maneras de contar. La combinatoria se puede definir como el arte de contar. Así lo hemos hecho en muchos posts precedentes. Sin embargo habría que hacer alguna precisión. No es lo mismo contar el número de ordenaciones de un conjunto finito de elementos que cumpla una propiedad concreta que contar los metros cuadrados que ocupa una superficie. La diferencia básica es que en el primer caso estamos en el dominio de los números enteros (o de los racionales si establecemos cocientes entre las cantidades previamente halladas), y en el segundo estamos en el dominio del continuo de los reales.

En cierto modo, estar en el dominio de R es cómodo: tenemos una serie de resultados que nos hacen agradable estar en el continuo de los reales, y que tienen que ver con temas topológicos muy profundos que ya se han discutido en el blog aquí.

Aunque es un tópico muy común, veremos que la integral de Riemann es una herramienta excelente para trabajar en "ambientes" en los que las buenas propiedades topológicas, tanto de los espacios como de las funciones a integrar, lo permiten. El problema vendrá cuando encontremos funciones, como la función de Dirichlet, que aunque definen problemas sencillos como el de encontrar la probabilidad de elegir un número racional al azar en el intervalo [0,1], no cumplen las "buenas propiedades" exigibles a las funciones para que sean integrables en el sentido de Riemann (las llamaremos funciones Riemann-integrables).

La meta será entonces encontrar una definición de integral que coincida con la de Riemann en las funciones Riemann-integrables, y que sea extensible a todas las funciones que se puedan definir de forma constructiva. Este reto es inmenso, y la forma de resoverlo me recuerda a la forma de Alejandro Magno de desatar el nudo gordiano. Para esta historia necesitaremos varios posts en los que recorreremos paisajes muy trillados y conocidos del cálculo diferencial; y otros menos conocidos y más exclusivos de la matemática menos "ingenieril".

Espero que sea un paseo agradable.

La paradoja de De Moivre (2 de 2)

En el post anterior vimos que cuando tiramos una moneda repetidas veces el cociente entre las caras y las cruces obtenidas tiende a la unidad. Más exactamente: dado un número ε , tan pequeño como queramos, la probabilidad de que dicho cociente diste de la unidad más de ε  tiende a cero al crecer n.

Lo vimos en el entorno de las leyes de los grandes números, y dijimos que en unas condiciones muy generales, las sucesiones de variables aleatorias cumplen dicha ley, que por otro lado es la que une la interpretación axiomática de Kolmogorov de la toería de la probabilidad, nacida de la teoría de la medida, con la interpretación frecuentista más intuitiva y universal.

A demás de ser la Teoría de la Probabilidad una parte importante y muy técnica de la matemática, existe una obvia cotidianeidad de sus aspectos más fundamentales con la vida actual de cada uno de nosotros. Todo el mundo entiende qué quiere decrie que un suceso tiene una probabilidadd dada, o al menos todo el mundo cree entenderlo. Lo que ocurre es que el anumerismo acecha detrás de muchas de las afirmaciones que se oyen en la calle, y éste es un terreno especialmente abonado para la proliferación de ideas anuméricas.

El teorema de Kintchine mencionado en el post anterior exige que una sucesión de variables aleatorias sea idénticamente distribuida (además de tener media finita). En estas condiciones se cumple la ley de los grandes números, y el cociente de resultados tiende con probabilidad uno a la probabilidad. Es importante entender que la condición resaltada es la usada en el teormea para la demostración, y que significa que todas las variables (todos los lanzamientos) son esencialmente idénticos. La moneda no tiene memoria, no sabe qué resultados se han obtenido anteriormente, ni existe ninguna ley de compensación que haga que tras diez caras sea más sencillo obtener una cruz. No hace falta en absoluto que tal ley de compensación exista para que las frecuencias de aparición se estabilicen alrededor de la probabilidad del suceso cuando aumenta el número de tiradas.

Ya lo he comentado en alguna ocasión: dos años de discusiones no fueron suficientes para convencer de ello a un jugador de lotería anumérico con el que compartía trabajo. Este pensaba que, ya que todas las terminaciones son igualmente probables y en media saldrán el mismo número de veces, si llevamos muchos sorteos sin que el número premiado acabe en cinco (por poner un ejemplo), la probablidad de que salga en el próximo es mucho mayor. Fruto de este tipo de creencias es la consideración de paradoja para la llamada "padadoja de De Moivre", que en realidad de paradoja no tiene nada, porque es extactamente lo esperable en ausencia de creencias anuméricas.

Repetimos el enunciado de la "paradoja":

Si lanzamos una moneda y anotamos el número de caras y cruces, progresivamente la razón de los dos números tiende a la unidad; y sin embargo la probabilidad de conseguir el mismo número de caras que de cruces tiende a cero.

Conseguir el mismo número de caras que de cruces (suponemos el núemro de lanzamientos n=2k par ) es un suceso cuya probabilidad no es muy difícil de hallar: Para empezar, con n lanzamientos tenemos 2ⁿ resultados posibles, al tener cada suceso dos posibilidades. Este es el número de ristras de n valores consecutivos "cara" o "cruz" posibles. Cuántos de estos tienen el mismo número de "caras" que de "cruces"?

Tenemos n=2k resultados individuales, que nos dan (2k)! permutaciones posibles. De los 2k resultados individuales k son iguales entre sí (caras), y los otros k restantes también (cruces). Cualquier permutación de los primeros k valores entre sí deja invariante el resultado, y lo mismo entre los k restantes. Dichas permutaciones lo son en número de (k!), luego el número total de resultados con igual número de caras y de cruces es (2k)!/(k!)(k!).

(2k!) es un número que crece muy rápido con k, pero si lo dividimos dos veces por (k!) la cosa crece más despacito. Dado que el número total de resultados es, como hemos dicho 2ⁿ = 2^2k, el cociente de ambas cantidades (2k)!/[2^2k(k!)(k!)] tiende a cero.

Demostrar esto no es difícil, si bien exige cierto cálculo de límites que no haremos aquí.

Así pues, la igualdad estricta de resultados es cada vez más difícil, mientras que el cociente entre ellos tiende a la unidad. De hecho, la tendencia a la unidad del cociente no implica la igualdad de resultados, ni ésta es condición necesaria para aquella, a pesar de las apariencias.

La paradoja de De Moivre (1 de 2)

 

Si lanzamos una moneda y anotamos el número de caras y cruces, progresivamente la razón de los dos números tiende a la unidad; y sin embargo la probabilidad de conseguir el mismo número de caras que de cruces tiende a cero. (Paradoja de De Moivre)

Pocos resultados hay en la teoría de la probabilidad tan globales, importantes y fáciles de entender (en su enunciado) como las Leyes de los grandes números. Sin embargo es muy corriente encontrar comentarios, razonamientos y anumerismos varios que demuestran que esta facilidad es engañosa.

Las leyes de los grandes numeros vienen a ser la justificación de la interpretación frecuentista de la probabilidad: si se realiza n veces un experimento y r representa el número de veces que se ha dado un determinado resultado, el cociente r/n tiende a estabilizarse alrededor de un punto p según va creciendo el número de pruebas,, que no es sino la probabilidad de dicho suceso.

Ilustraremos esto con el lanzamiento de una moneda, suceso simple donde los haya:

Los sucesivos resultados del experimento repetido n veces se pueden expresar mediante una colección de  n variables aleatorias X₁,..., X_n. Si no existe relación entre un experimento y los siguientes diremos que son independientes (sacar una cara a la cuarta tirada no influye en los resultados de las siguientes tiradas). En estas condiciones, las variables X₁,..., X_n tienen la misma distribución. Cada una de las X_i tiene, como variable aleatoria que es, una media y una varianza. Llamaremos E[X_i] a la media o esperanza de la variable X_i.

En estas condiciones, llamaremos en un alarde de imaginación media muestral a

Y_n= 1/n · (X₁+...+ X_n)

Es evidente que Y es también una variable aleatoria, que tendrá su media y su varianza.

Llamaremos a_n = E [Y_n] al valor esperado de la media muestral.

Diremos que una sucesión de variables aleatorias X₁,..., X_n cumple la ley fuerte de los grandes números cuando

Y_n - a_n → 0 casi seguro.

Dicho en lenguaje coloquial: la probabilidad de que Y_n diste de a_n un valor e tiende a cero al crecer n, por pequeño que sea e.

Los sucesivos teoremas sobre la ley de los grandes números no hacen sino investigar las propiedades (muy generales) que deben cumplir las variables aleatorias para que cumplan efectivamente la ley. Es importante resaltar que el enunciado anterior es un enunciado probabilístico sobre teoría de la probabilidad. Nos está hablando de una probabilidad asintóticamente nula para un suceso muy concreto relacionado con la media muestral de una colección de observaciones.

Esta ley es cumplida por la mayoría de las variables aleatorias usuales, “de buen comportamiento”, y nuestro experimento de lanzamiento de monedas la cumple, entre otros, por el llamado Teorema de Kintchine que dice que:

Si X_n es una sucesión de variables aleatorias independientes e igualmente distribuidas con media finita, entonces se cumple la ley fuerte para dicha sucesión de variables aleatorias .

El nivel de exigencia del teorema de Kintchine es realmente bajo: las variables deben ser independientes (un lanzamiento no influye en los siguientes), y las variables deben tener media finita. Hay versiones incluso más generales, que hacen que la ley se cumpla en casi todos los casos no patológicos.

En nuestro caso, dado que cada experimento tiene dos posibles resultados (cara o cruz, que asimilaremos a los valores 0 y 1 de las variables) con idéntica probabilidad, cualquiera de las X_i tiene una distribución de Bernoulli, con

P{ X_i = 0 } = 0.5

P{ X_i = 1 } = 0.5

Y por tanto E[X_i ] = 0.5

a_n = E[Y_n] = 1/n.( E[X₁ ]+ ... + E[X_n ] = (1/n) . (n/2) = 0.5

Luego en nuestro caso la ley fuerte de los grandes números nos indica que para n suficientemente grande, la probabilidad de que la media muestral se desvíe de 0.5 en una cantidad no nula es menor que cualquier infinitésimo e. No importa lo ínfimo de la desviación, si el número de pruebas es suficientemente grande, la media muestral caerá dentro del intervalo (0’5 - e , 0’5 + e ) .

 

Dado que estamos evaluando la esperanza de la variable [Y_n], media muestral; este resultado nos indica que la fracción de caras será el 50% del total, y cruces el otro 50% del total.

Otra forma de decir lo mismo es que el cociente del número de los resultados “cara” por el número de los resultados “cruz” se separe de la unidad tan poco como queramos, con sólo aumentar el número de pruebas.

¿Quiere esto decir que el número de caras y de cruces va a ser exactamente el mismo si tiramos un número enorme de veces (enorme y par)?

Pues no. No sólo no quiere decir esto, sino que la realidad es que la probabilidad de que los lanzamientos empaten decrece hacia cero con n.

Demostrar esto y comentar las implicaciones de la paradoja de De Moivre será objeto del próximo post.

 

 

Siguiente término de una sucesión (2/2)

Segundo post de la serie, a cargo de Jorge Alonso.


En uno de sus libros, John Allen Paulos comenta de pasada un método para hayar una ley matemática que haga que el siguiente término de la sucesión sea el que queramos que sea. La clave se encuentra en que la serie de partida es una serie finita.

Para evitar una explicación farragosa, partamos de una serie inicial de tres términos

a, b, c

en la que queremos que el siguiente término sea d.

El término general será f(n); partamos de

f(n) = a + b + c

Cuando n = 1, esta expresión debe valer a, por lo que multiplicamos a los valores b y c por unos ceros camuflados:

f(n) = a + b(n-1) + c(n-1)

Para n = 2, debe cumplirse que f(2) = b

f(n) = a(n-2) + b(n-1) + c(n-1)(n-2)

Y lo mismo para n = 3:

f(n) = a(n-2)(n-3) + b(n-1)(n-3) + c(n-1)(n-2)

Aún no hemos acabado, ya que, por ejemplo, para n = 2 no obtenemos

f(2) = b, sino

f(2) = b(2-1)(2-3)

por lo que hay que dividir cada término por factores correctores:

f(n) = a(n-2)(n-3)/(1-2)(1-3) +
+ b(n-1)(n-3)/(2-1)(2-3) +
+ c(n-1)(n-2)/(3-1)(3-2)

Ahora sí que hemos obtenido una expresión f(n) que cumple con los términos iniciales. De forma análoga, podemos añadir nuestro nuevo término d:

f(n) = a(n-2)(n-3)(n-4)/(1-2)(1-3)(1-4) +
+ b(n-1)(n-3)(n-4)/(2-1)(2-3)(2-4) +
+ c(n-1)(n-2)(n-4)/(3-1)(3-2)(3-4) +
+ d(n-1)(n-2)(n-3)/(4-1)(4-2)(4-3)

Sabiendo este truco matemático ya no habrá serie que se nos resista, ni siquiera las que aparecen en los test de inteligencia.

 

Siguiente término de una sucesión (1/2)

Lo siguiente es una colaboración de Jorge Alonso, habitual en el blog. Es una serie de dos posts, en la que nos explica cómo encontrar el siguiente término de una sucesión, dados unos términos iniciales.

Un conocido pasatiempo consiste en, dada una serie de números,averiguar cuál es el siguiente, cumpliendo el orden lógico de la serie.

Por ejemplo, si la serie es

1, 3, 5, 7, 9

el siguiente término es 11, ya que se trata de una sucesión de número impares. El término general de esta serie puede escribirse como

f(n) = 2n - 1

valiendo n sucesivamente los valores 1, 2, 3, 4...

Otro ejemplo es

0, 1, 1, 2, 3, 5, 8, 13

en el que cada término es la suma de los dos precedentes, comenzando por 0 y 1. Puede expresarse esta serie como

f(0) = 0
f(1) = 1
f(n) = f(n-1) + f(n-2)

Veamos un ejemplo más:

1, 1, 2, 2, 4, 3, 8, 4, 16, 5

Parece más difícil, pero basta un truco para hayar la lógica: separar la serie en dos, tomando términos alternos:

1, 2, 4, 8, 16

1, 2, 3, 4, 5

Por tanto, el siguiente término es 32. El término general es:

2^((n-1)/2) si n es impar

n/2 si n es par

Sin embargo, siempre puede encontrarse otra lógica distinta a los números de la serie, con lo que el siguiente término sería otro distinto. Y esto puede hacerse de forma que el siguiente término sea el que nosotros queramos que sea.

Sea, por ejemplo, la sucesión

0, 1, e, pi

queremos que el siguiente término de la serie sea i, ¿cómo podremos lograrlo?

 

Respuestas ciertas, pero insatisfactorias

A veces una respuesta puede ser impecablemente cierta, y sin embargo insatisfactoria. Ese es el caso del alumno que respondíó en esta pregunta de examen.

PD.- Ese es también el caso de TioPetros cuando le preguntan porqué lleva un mes sin actualizar la bitácora. Tengo mil motivos, todos válidos pero todos insatisfactorios. Espero poder volver en breve con todos ustedes. Por cierto; las visitas no dejan de subir desde que no escribo. Realmente, no sé cómo tomármelo...

 

 

Anuncios

Sé que no tengo derecho a reclamación. Blogia no me pide un duro y me aloja el blog desde hace más de dos años. Comprendo perfectamente que es inevitable algo de publicidad, y si sirve para que el proyecto Blogia sea menos oneroso, o incluso rentable, me alegro.

Pero en fin, a poco que me vayan conociendo supondrán que ver este anuncio en mi blog no me hace ninguna gracia.

(Gracias Luis MIguel por el aviso)

Steven Weinberg opina sobre el principio antrópico

En este blog hemos hablado varias veces del Principio antrópico . Casi siempre para explicar que no me parece un principio que deba ser tomado excesivamente en serio.

Las teorías del diseño inteligente no son sino versiones particularmente teológicas y teleológicas de este principio antrópico, y últimamente están teniendo un eco mediático importante. Antes que que algún lector enervado me tache de inquisidor, censor o algo peor, debo decir que a mi me parece muy bien que grupos de personas vayan por ahí haciendo apología de sus opiniones (mientras dichas opiniones estén dentro de la ley) y que apoyo cualquier iniciativa conducente a que tengan derecho a expresarse y a publicar su ideología. Pero del mismo modo apoyo y ejerzo el derecho a denostar aquellas opiniones que me parecen falsas. Esa es toda la cuestión.

Pues bien, acabo de encontrar unas reflexiones en la red, publicadas con Carlos Sanchez Chinea, en su página que ya hemos recomendado alguna vez por su extraordinaria calidad y claridad. Estas reflexiones son del premio Nobel Steven Weinberg. Steven Weingerg es Profesor de Física, Universidad de Texas en Austin, Ganador del Premio Nobel de Física en 1979.

Por supuesto, no les comento esto simplemente por un principio de autoridad; un premio Nobel puede decir tantas sandeces como cualquiera. Pero es que me gusta mucho cómo el profesor Weinberg aborda el tema; y me alegra leer unas reflexiones que coinciden con las mías cuando están realizadas por alguien de probada solvencia en el mundo del pensamiento.

Tienen el artículo aquí. Como explica Sanchez Chinea, Este artículo se basa en una charla dada en Abril de 1999 en la Conferencia sobre el Diseño Cósmico por la Asociación Americana para el Avance de la Ciencia en Washington, D.C. y publicado en la New York Review of Books .

Einstein, annus mirabilis. Jornada 2 (7)

Tercera charla de la tarde del día 7.



Jean Marie Lehn Premio nobel 1987 por sus estudios sobre las bases moleculares del reconocimiento celular.

Pasos hacia la materia compleja: información, auto-organización y adaptación en sistemas químicos

Esta ha sido una charla para mi sorprendente. Es la primera vez que oigo hablar de adaptación prebiótica. La charla parte de la intrigante y terrible pregunta siguiente:

¿Cómo es posible que la materia y la energía generadas en el Big Bang, con las leyes de la relatividad general y las demás leyes físicas pueda haber ganado en complejidad hasta generar un organismo pensante capaz de idean precisamente la relatividad general?( en alusión al organismo que conocemos como Albert Einstein)

La respuesta pasa por comprender que la materia evoluciona bajo "presión de información"; la propia estructura de la materia tiene las pripiedades necesarias para su autoorganización, y a todos los niveles: la autoorganización se revela como un imperativo cósmico.

A nivel cosmológico existe autoorganización en los grandes conglomerados de materia bajo influjos de la gravedad.

Al nivel inferior es bajo el influjo electromagnético que se autoorganiza la materia en atomos, moleculas y agregados moleculares.

De las moléculas a la química celular el estudio de la química tridimensional ha revelado que las bases de reconocimiento entre células, entre células y virus o entre células y anticuerpos son bases químicas en las que moléculas superficiales reconocen sus dianas mediante mecanismos explicables con la analogía de la llave y la cerradura: es la propia configuración tridimensional de las moléculas la que hace el trabajo.

Se hace un repaso a la eficacia del ADN como almacén de información, y se afirma que este sistema de reconocimiento llave - cerradura parece implicar un prediseño, pero nada hay más lejos de la realidad: se trata de sistemas autoorganizativos.

Pone como ejemplo la estructura del virus del tabaco. Su envoltura está formada por un tubo hueco que contiene el ARN en su interior. El tubo está formado por ladrillos idénticos que se van agregando en espiral formando así el tubo. El concepto importante es que es la propia superficie del ladrillo individual el que dicta la unión de cada ladrillo con el siguiente. La pauta helicoidal que forma el tubo hueco del virus surge espontáneamente de dichas uniones sin necesidad de ningún diseño añadido.

En nanotecnología el autoensamblado de este tipo evitaría las dificilísimas tareas de ensamblado, consiguiéndose por autoorganización la construcción macromolecular deseada.

Por medio de la autoorganización los conceptos cambian. Concretamente, en lugar de
fabricación hablaremos de autoensamblado , en lugar de reparación hablaremos de autoreparación , en lugar de direccionamiento hablaremos de autoconexión y en lugar de manipulación hablaremos de adaptación

Efectivamente, según el ponente se puede hablar de selección y de adaptación prebiótica (o abiótica?) la autoorganización a nivel químico.

Esto da otra pista de la posible forma de fabricación de dispositivos nanotecnológicos en sistemas de tipo llave-cerradura. En lugar de fabricar la llave que necesitamos, fabricamos aleatoriamente un número ingente de posibles llaves, con un mecanismo que amplifique la producción de la configuración concreta que habra la cerradura. Genramos variabilidad para que hata selección. Estamos en terreno de la Química constitucional dinámica.

En una charla anterior se ha dicho que la química era la ciencia del siglo XIX, la física y la biología del XX y la nanotecnología la del XXI. El profesor apunta que según su opinión la química será la ciencia del siglo XXV.

Acaba con la frase de David Hilbert: "Wir müssen wissen, wir werden wissen"

Debemos saber, sabremos.

Einstein, annus mirabilis. RESTO DEL CONGRESO

La segunda charla de la mañana ha estado a cargo de Cliffor M. Will , y es una continuación de la que dió la víspera, de modo que la reseña para ésta sirve para ambas.

El diseño del congreso ha sido tan bueno que no ha faltado tampoco la componente humana de Einstein, ni la vertiente filosófica o el impacto en el mundo de la cultura de su trabajo. Las últimas ponencias del congreso se han dedicado a estos aspectos, me dediqué a disfrutarlas sin tomar notas, de modo que antes que dar una crónica parcial de la misma prefiero no hacerlo en absoluto. Tan sólo comentar que un servidor opina que si la vertiende humanística hubiera estado ausente del congreso, habría quedado cojo sin remedio.

José Mª Sanchez Ron habló sobre Einstein y la filosofía del siglo XX ; Gerald Holton lo hizo sobre el lado humano del científico en su ponencia Einstein: ¿quién pensó que era y porqué sigue aún vivo hoy en día y Arthur I. Miller , marcó un paralelismo entre las vidas y obras de Picasso y Einstein. Las tres fueron de extraordinario interés, en mi modesta opinión especialmente la de Holton.

De la última ponencia, de John Jay Stachel titulada El gran sueño de Einstein: Una física independiente no puedo hablar por no haberla escuchado.

Aquí acaba la crónica que he podido realizar de este congreso. Creo que ha sido un acontecimiento científico de nivel mundial, y por unos días me he sentido orgulloso de vivir donde vivo. Es una sensación que no se prodiga mucho, y es maravillosa.



_{En la foto, una instantánea del público que abarrotó en todo momento el salón del actos del Kursaal}

El muchacho que tenía una teoría

Me van a permitir una reflexión sobre una vivencia del reciente congreso sobre el annus mirabilis einsteniano, del que hemos dado cumplida información en los posts anteriores.

El primer día, nada más recoger la información, me senté en un sillón del hall para repasar el programa, mientras a mi lado dos chicos de unos dieciseis años hacían exactamente lo mismo que yo. La última actividad del primer día era un cóctel de bienvenida.

-Eso, eso, el cóctel- le dijo uno de ellos a su compañero- allí podremos encontrar a quién contar mi teoría.

Hostias!, pensé: uno que tiene una teoría.

El caso es que la pareja de amigos no se perdieron una charla, y se convirtieron en parte habitual del paisaje congresístico...hasta que en El diario Vasco salió el muchacho en la crónica diaria que dicho periódico dedicaba al evento.

Cada día los reporteros escogían a varios congresistas y les hacían una breve entrevista sobre sus impresiones en el congreso; ya saben, esas cosas que hacen los periódicos y que sirven para adornar la crónica.

El caso es que al chaval le faltó tiempo para contar que él también tenía una teoría, y al día siguiente era poco menos que una pequeña celebridad en un congreso en el que había seis premios Nobel.

No pude resistirme, y me acerqué para charlar con él. Comencé por darle la enhorabuena de corazón: era un placer ver a dos chavales de dieciseis años fieles al horario del congreso, sin perderse una charla. Como era inevitable, en breve el tema de conversación pasó a su teoría.

Hacía todavía poco que había tenido un encontronazo en otro ambiente con alguien que también tenía una teoría. En realidad aquel tenía varias, una mejoraba la Teoría de la relatividad y otra enmendaba la plana a Darwin.

Una de las cosas que he aprendido de los que quieren suponer un cambio de paradigma en la ciencia desde su autodidactismo es que no sirve de nada discutir con ellos. Para empezar, porque el entendimiento es imposible: manejan un vocabulario propio fruto del autismo que supone elucubrar alejado de la producción científica de los que realmente hacen ciencia.

Este caso era diferente. Para empezar era diferente por la juventud de los muchachos. No estaban maleados, es evidente que eran inteligentes, y se notaba que sentían un verdadero amor por la ciencia.

Pero cuando comenzó a hablarme de su teoría, volvieron las imágenes de mis anteriores discusiones: no era posible entender nada. Supongo que la cosa se trataba de superar la velocidad de la luz, porque se refería el chaval una y otra vez a "la barrera".

Me confirmó que la víspera había conseguido hablar con el profesor Echenique, organizador del congreso y director del Donosti International Physics Center , y éste le había dicho que le mandara su teoría por email.

Le escuché, y al final le comenté el tema de la nomenclatura: es importante llamar a las mismas cosas por el mismo nombre; le dije que lo tuviera en cuenta a la hora de escribirle al profesor Echenique.

Además de inteligente era muy amable, así que me agradeció el consejo.

En cuanto dejaron de hablar conmigo los abordó una señora muy simpática con profundo aspecto de ser profesor de física, que les preguntó con enorme cariño sobre la entrevista en el periódico de la víspera, y les dijo que era un placer ver gente tan jóven en el congreso. Se habían convertido en conocidos de todo el mundo.

Los ví marchar, y dos pensamientos luchaban en mi cabeza:

El primero era que cuanto antes se diera la torta con su teoría, mucho mejor para él. Si dentro de diez años seguía creyendo "tener una teoría", mala cosa.

El segundo era que si ese chaval fuera hijo mío, yo hubiera estado muy orgulloso de él.

Einstein, annus mirabilis. Jornada 3 (6)

TERCERA PONENCIA DE LA TARDE


CLIFFORD M. WILL Washington University

¿TENIA RAZON EINSTEIN?

La trascendencia de la teoría de la relatividad ha empujado a algunos autores a manifestar que el mundo moderno empezó el 29 de mayo de 1919, el famoso día del eclipse por medio del cual Sir Arthur Eddington demostró experimentalmetne la validez de (al menos la primera de) las afirmaciones de la Teoría General de la Relatividad.

Sin embargo y a pesar de las impresiones en contra, la teoría entró en declive a una velocidad enorme hasta que volvió a resurgir ya entrada la década de los sesenta del siglo XX por razones que se explican en la propia charla del profesor Will.

Los motivos de dicho declive, prejuicios más bien, son principalmente dos:

1.- La idea de que la teoría es extraordinariametne difícil de entender, propiciada en parte por el propio Eddington al no estar de acuerdo con la afirmación de un periodista de que sólo tres personas entendían dicha teoría. El desacuerdo era no lo exiguo de número, sino la mera existencia de un tercero.

2.- Se pensaba que aparte de unos pocos efectos, la TGR no tenía casi ningún contenido experimental.

Esto hizo que incluso Einstein hiciera desafortunadas (¿Y quizás espurias?) afirmaciones exclamando que si los datos no avalaban su teoría, peor para los datos: la teoría era correcta.

Faltaba un interfaz entre la teoría y los hechos, y este interfaz llegó en los años sesenta en cuatro aspectos de la astronomía:

1.- El descubrimiento de los cuásars (1961)

2.- El descubrimiento de la radiación de fondo de 3 K (1964)

3.- El descubrimiento de los pulsars (1967)

4.- El descubrimietno de los agujeros negros (1971)

Se reescribió la TGR en términos modernos más acordes con la observación. Esto unido a la revolución tecnológica que propición instrumentos de precisión antes impensable produjo la posibilidad de nuevos experimentos para verificar la teoría.

Estos experimentos que testean la TGR se clasifican en cuatro apartados:

1.- Curvatura de la luz en presencia de objetos masivos

2.- Evaluación fina de la precesión real del perihelio de Mercurio

3.- Efecto de arrastre del espacio tiempo por el giro de un objeto masivo.

4.- Efectos gravitatorios.

Un resumen sucinto de los datos aportados por el profesor Wills sobre la precisión alcanzada en las medidas actuales puede ser la siguiente, escrita a vuelapluma y sin la debida fidelidad a la exacta exposición que nos ha brindado tanto en esta exposición como en la de la mañana del día 8 (complementaria a ésta) podría ser más o menos así:

1.- Tests de que la velocidad de la luz es la máxima que puede alcanzar un cuerpo al que se le inyecta energía (INVARIANZA LOCAL DE LORENTZ)):
probado con precisión de diez a la menos 21 (una parte en una miltrillonésima) en 1990, mientras que Michelson y Morley lo consiguieron con una precisión de uno entre mil.

2.- (WEAK PRINCIPE OF EQUIVALENCE) Tests sobre el principio débil de equivalencia; osea: que todos los graves caen con la misma aceleración:
probado experimentalmetne hasta precisión de diez a la menos doce (dos partes en un billon)

3.- Valor unidad del coeficiente gamma de deflexión de la luz en presencia de campos gravitatorios (TGR) Probado por el efecto de retraso de Shapiro (la señal llega más tarde al seguir un camino curvo) con precisión actual de diez a la menos cinco.

4.- Comprobación del efecto arratre de un cuerpo masivo rotatorio en el espacio tiempo: acuerdo absoluto entre observación y teoría, si bien no he recogido la máxima cifra de error.

5.- Precesión del perihelio de mercurio con los datos más modernos de órbitas y masas planetarias y solar, en relación a lo observado: ACUERDO ABSOLUTO, DISCREPANCIA DENTRO DEL ERROR EXPERIMENTAL. Los datos son: Teoría: 42,98 +- 0,04 segundos de arco por siglo, (descontado el efecto conocido de perturbación de otros planetas ). Valor observacional obtenido: 42,98)

6.- Pérdida de energía orbital de pulsars por emisión de ondas gravitacionales: los valores observacionales se ajustan a la curva teórica de tal manera que parece que la curva teórica es el mejor ajuste concebido estadísticamente sobre los puntos observacionales en lugar de ser simplemente eso: una curva predicha por la teoría. (ver ilustración)



Así pues, parece ser que según los datos más recientes y en los márgenes de error instrumental actuales la respuesta a la pregunta que titula la ponencia es afirmativa.

Einstein, annus mirabilis. Jornada 3 (3)

TERCERA PONENCIA DE LA MAÑANA.



PONENTE: FRANCISCO JOSE YNDURAIN (Univ. autónoma de Madrid)
RELATIVIDAD, FOTONES Y PARTÍCULAS

Esta ponencia ha sido una absoluta gozada. El profesor Yndurain, con una presentación a base de transparencias, (sin PowerPoint!!!), y ayudado de un paraguas como puntero ha dado una charla magistral sobre la labor de Einstein a lo largo de toda su vida, y especialmente de cómo vivió el auge de la mecánica cuántica que él había ayudado a nacer mientras se dedicaba en vano a encontrar una teoría de campo unificado.

Comienza la charla con un nuevo repaso a las contribuciones de Einstein en el annus mirabilis de 1.905, centrado en tres logros:

1.- El estudio de la naturaleza del movimiento browniano.

2.- La relatividad especial.

3.- El efecto fotoeléctrico.

Cualquiera de los tres por separado hubiera encumbrado a Einstein al parnaso de los científicos inmortales. El profesor Yndurain ataca dos mitos biográficos de Einstein: sus malas notas y la falsa y ubicua afirmación de que creó sus teorías de la nada. Albert Einstein por el contrario gozó de una formación extraordinaria.

Su vida se puede dividir en tres etapas:

1.- La etapa difícil de los comienzos. No es admitido en la politécnica de Zürich. En 1.902 ingresa en la oficina de patentes de Berna, donde sigue en 1.905 cuando publica sus tres trabajos tantas veces mencionados en estos días de congreso.

En 1.915 publica la Teoría General de la Relatividad, en lo que según muchos es el más bello trabajo científico jamás escrito.

2.- El éxito. Tras el eclipse de 1.919 Sir Arthur Eddington demuestra la corrección de las afirmaciones einstenianas en relatividad general, consiguiendo un éxito mediático sin precedentes, llegando a tener ribetes ridículos a lo largo de su vida, como la propuesta de presidencia del estado de Israel.

En 1.921 recibe el premio Nobel, por su artículo sobre el efecto fotoeléctrico de 1.905 no admitido por la comunidad científica hasta 1920 tras las confirmaciones de Compton.

3.- El declive

Einstein se enfrasca infructuosamente en la teoría del campo unificado, mientras a sus espaldas la mecánica cuántica crece imparable. En 1932 Pauli se atreve por primera vez a criticar a Einstein de maner sarcástica. Einstein ya no sigue la física contemporánea, teniendo más importancia como icono social y como referente moral que científico.

El profesor Yndurain pasa a explicar el cambio brusco de perspectiva que suponen las contribuciones de Einstein a inicios del siglo XX.

Existía una contradicción muy profunda entre las teorías de la mecánica (Galileo-Newton) y el electromagnetismo de Maxwell: por un lado estaba la ley aditiva de composiciónd e velocidades;

v = v₁ + v₂

pero de las ecuaciones de Maxwell se extraía sin esfuerzo el siguiente resultado:



lo cual daba a la velocidad de la luz en el vacío un valor constante igual al inverso de la raíz cuadrada del producto de las permisividades eléctrica y magnética del vacío (o del medio a considerar).

Esta invarianza respecto a la fuente emisora está ya implícita en la teoría maxwelliana, y no se comprendía en absoluto aunque se conocía sobradamente.

Las explicaciones, simpre ad hoc, pasaban por postulaciones insatisfactorias de un eter que llenaba el espacio; pero tras el resultado del experimento de Michelson y Morley se hacía necesaria una reformulación.

Ya Lorentz había postulado la contracción longitudinal para explicar el resultado de dicho experimento:



y Poincaré había hecho notar que tal contracción iría acompañada de una dilatación temporal por el mismo factor, con lo que las transformadas de Galileo quedarían transformadas en lo que hoy se conoce como transformadas de Lorentz:



Una de las cosas que hace Einstein, en palabras del profesor Yndurain, es darle la vuelta al calcetín. Eleva la constancia de la velocidad de la luz a categoría de axioma, demostrando que tan sólo con este gérmen ya implícito en Maxwell se puede llegar de forma bien sencilla a las transformaciones de Lorentz, y demostrando además que la masa de los cuerpos aumenta con la velocidad, y llegando a la fórmula estrella de la física de todos los tiempos:

e = mc²

El efecto fotoeléctrico

El hecho de que la luz azul arranque electrones de superficies materiales más energéticos que la roja, con independencia de la intensidad del rayo luminoso, intensidad que tan sólo influirá en el núemro de electrones arrancados; es algo que no tenía explicación en la teoría clásica.

En 1.905 Einstein postula los fotones, que él llamó licht quanten , cuantos de luz.

Su teoría no fué aceptada hasta los trabajos de Compton de 1.920, siendo citado el trabajo de Einstein como una de sus veleidades científicas. Sin embargo dos años después recibía el nobel por esta contribución. El propio Planck diría en un momento que aceptaba los cuantos de luz como un acto de desesperación

En 1.923 Louis de Broglie aumenta el estupod de la dualidad onda-corpúsculo aformando que el electrón, y por extensión cualquier cuerpo móvil se comporta como una onda de una longitud determinada por su momento (Longitud de de Broglie).

Esta dualidad añadida a la no localidad empezaba ya a molestar a Einstein...

Consideraciones sobre la Teoría General de la Relatividad.

El profesos Yndurain menciona el nuevo marco que supone la TGR a la hora de explicar la gravedad por medio de geometría del espacio tiempo. Su nueva teoría, una de las construcciones teóricas más bellas que ha realizado la especie en toda su existencia, da cuenta de fenómenos inexplicables como la precesión del perihelio de mercurio (tema tratado en extensión por otro conferenciante más tarde), así como la deflexión de la luz al pasar por las inmediaciones de un cuerpo masivo. La confirmación experimental de esto último con el famoso eclipse de Eddington es de sobre conocido.

Termina la charla expliando la obsesión de Einstein por una teoría de campo unificado, y ante una pregunta del público en este sentido, el profesor Yndurain afirma que se está tan lejos de integrar la gravedad en las demás fuerzas fundamentales como hace ochenta años.

Las tentativas actuales son eso: tentativas, y todas ellas pasan por la mecánica cuántica. Hoy, que se sabe mucho más que entonces, cualquier intento de unificar mediante geometría (idea einsteniana) ha quedado abandonado, siendo las interacciones entre partículas a nivel mecanocuántico relativista el caballo de batalla actual, lo que indica claramente que en este aspecto Einstein estaba equivocado.

Einstein, annus mirabilis. Jornada 4 y última (1)

PRIMERA CHARLA DE LA MAÑANA

PEDRO PASCUAL Universidad Central, Barcelona

EINSTEIN Y LOS CUANTOS DE LUZ

En esta charla el profesor Pascual nos explica las dos contribuciones de Einstein sobre los licht quanten , como denominó a los fotones.

Por supuesto, el primero de los trabajos es el ya innumerables veces a lo largo del congreso nombrado trabajo de 1.905 sobre el efecto termoiónico que le llevó a recoger el Premio Nobel en 1.921 tras las confirmaciones del efecto Compton.

En el efecto fotoeléctrico había una mezcla de eectos, algunos de los cuales podían ser bien explicados a la luz de la teoría clásica, pero otros no.

De la primera clase eran los efectos siguientes:

1.- El número de electrones producidos es proporcional a la intensidad de la luz.

2.- La emisión de electrones es instantánea con la luz.

Pero no podían explicarse en absoluto los siguientes.

3.- Por debajo de una frecuencia umbral de luz monocromática no se producía la emisiñon de electrón alguno.

4.- La energía cinética de los electrones producidos era proporcional a la frecuencia de la luz monocromática utilizada.

Einstein postula que los cuantos de luz monocromática ceden energía a los electrones para liberarse (hoy diríamos para abandonar su órbita). Los cuantos de luz portan una energía directamente proporcional a su frecuencia (color).Por debajo de una energía (o frecuencia) mínima para hacerlo simplemente no hay electrones que se puedan liberar. Por encima de dicha energía, el resto de energía sobrante es la energía cinética que se llevará el electrón. Dado que la interacción es de un cuanto de luz con un electrón, el aumento de frecuencia (energía) del cuanto no implicará más electrones, sino electrones más energéticos, con una energía igual a la del cuanto menos la necesaria para liberarse.

La reticencia para aceptar estos resultados, que fueron catalogados por el propio Einstein como la más revolucionaria de sus ideas cinetíficas no sólo no fué inmediata, sino que tardó 16 años en llegar.

Muestra de la reticencia es una carta de recomentación para Einstein que escribió en 1.913 Max Plank, en la que se podía leer:

Que algunas veces se haya equivocado en sus especulaciones, como por ejemplo con los cuantos de luz no puede ser tenido en contra suya..."

Poco a poco la comunidad cientñifica va admitiendo la hipótesis de los cuantos de luz. Millikan por ejemplo admite que tras desperdiciar 10 años de su vida luchando contra la idea termina por aceptarla por buena.

Los estudios de Arthur Compton sobre el efecto que lleva su nombre terminarán por levantar los imodimentos a una aceptación completa, lo que provoca la concesión del premio Nobel para Einstein en 1.921

La palabra fotón sin embargo no se hará un lugar en la ciencia hasta 1.925, año en que la introducirá con fortuna Lewis.

El otro gran trabajo deEinstein sobre los cuantos de luz es de 1.927 y tiene relación con los cálculos de los coeficientes de absorción inducida y emisión espomtánea e inducida en un gas atómico radiado por luz.

Este trabajo es el gérmen de las teorías del laser y el maser, que desarrollaron Schawlow y Townes en 1958. Ninguno de los dos pensó realmente en aplicaciones prácticas del laser, tan ubicuo hoy en día."

Einstein, annus mirabilis. Jornada 3 (5)

SEGUNDA PONENCIA DE LA TARDE



ANTHONY HEWISH. Premio nobel física 1.974
FISICA DE LOS PULSARES Y ENSAYOS DE EINSTEIN

Es sin duda toda una experiencia oir hablar de algo tan mítico como el descubrimietno de los púlsares, cuando el ponente habla en primera persona. Eso es lo que se ha oído esta tarde en Donostia. Hewish ha glosado su descubrimiento (codescubrimiento con su estudiante Jocelyn Bell-Burnell, habría que decir) de forma muy atrayente y amena. Afirma que todo esto a Einstein le habría encantado . Desgraciadametne, el descubrimietno se realizó en 1.967, demasiado tarde para el físico genial.

Explica el interés de los púlsars por al menos dos propiedades de los mismos:

1.- Presentan campos gravitatorios extraordinariamente potentes, lo que los hace ser unos perfectos laboratorios para testear la Teoría General de la relatividad.

2.- Proporcionan un método de medición de tiempo extraordinariametne regular.

A lo largo de la charla, el profesor Hewish presenta la nebulosa del Cangrejo como el resto de una explosión de supernova ocurrida en 1.054 ( en ese año llegó a la tierra la luz procedente de la explosión, matiza). Un estudio de las velocidades de la envoltura estelar lanzada por la explosión indica de forma certera el origen de todo ello: en dicho punto existe una estrella extraordinaria que emite en banda ancha incluido el espectro visible(hecho no corriente en los pulsares). La estrella emite destellos de frecuencia de milisegundos, lo que indica una estrella masiva de dimensiones mínimas que gira muy rápido, a la vez que emite en direccionalmente. Cuando el rayo emisor barre la zona de la tierra vemos el destello.

Explica que el descubrimiento se realizó mientras buscaban galaxias que presentaban un efecto de titilación análogo al que presentan las estrellas por culpa de factores atmosféricos, mientras los planetas no los presentan por no parecer objetos puntuales. Con los cuasars pasa algo parecido, pero el culpable es el viento solar.

Sin embargo se detectó el 6 de agosto de 1.967 una fluctuación con un 100% de variación de intensidad respecto a la componente fija de la misma a medianohce, momento que excluye lausas solares. Tras ser observado varias veces y regustrado mediante registradores del momento (de pluma de tinta), y trasw cambiar los registradores y ratificar la observación surge la estravagante posibilidad de emisiones inteligentes.

Esto se desechó cuando no pudo observarse efeco Doppler alguno que indicara que la emisión provenía de un planeta en rotación a una estrella. La hipótesis que restaba debía ser la buena: una estrella muy densa, quizás una enana blanca, pero más posiblemente una estrella de neutrones.

Explica en profesor Hewish que el principio el exclusión de Pauli para fermiones impide que cuando una estrella se condensa (una enana blanca por ejemplo) los electrones se apilen densamente. A pesar de esto, si la presión continúa aumentando se da un proceso de combinación de un protón con un electrón:

p⁺ + e^- = n⁰ + v (neutrino)

este proceso es inverso al de degeneración de un neutrón en un protón y un electrón, suceso más corriente.

Cuando esto sucede, nada impide a un nuevo colapso, formándose una jalea de neutrones ultradensa (del orden de mil millones de toneladas por centímetro cúbico) , que por conservación del momento angular debe girar vertiginosamente.

Tras describir la estructura posible de estas estrellas, consistente en una corteza de materia degenerada normal (esto es: análoga a la de una enana blanca, sin la reacción anteriormente citada); un manto neutrónico y quizás un núcleo de quarks libres; el profesor Hewish pasa a describir los efectos de relatividad general en un sistema binario formado por dos estrellas de este tipo.

Menciona al menos tres efectos en su charla:

1.- La emisión de ondas gravitacionales por los objetos masivos que giran uno alrededor del otro

2.- La precesión orbital.

3.- La precesión geodésica, o precesión del eje de giro de los objetos sobre sí mismos.

Respecto a la emisión de ondas gravitacionales, aclara que nunca se han observado directamente; sin embargo la pérdida de energía orbital de estos sistemas, perfectamente medible, se muestra finamente ajustada a lo esperable por emisión de dichas ondas.

Menciona valore obtenidos para las precesiones orbitales de ciertos sistemas binarios como PSR 1913+16 (Hulse y Tyler, 1973, Arecibo), con un período de 59 milisegundos. Esto significaba que el PSR 1916+13 era el sistema idóneo para el estudio de sistemas orbitantes sobre campos gravitatorios fuertísimos.

La excepcional estabilidad de la velocidad de giro de algunos sistemas binarios parecidos es tal que el período del sistema conocido como PSR1937+21 se haya cifrado en 1,55780644887275 milisegundos, con un error máximo de tres en su última cifra decimal, lo que habilita a estos sistemas como relojes de precisión prácticamente insuperable.

Einstein, annus mirabilis. Jornada 3 (4)

PRIMERA PONENCIA DE LA TARDE.



SHELDON LEE GLASHOW Universidad de Boston, Premio Nobel 1.979

¿QUE ES UNA TEORÍA UNIFICADA?

La conferencia trata sobre la búsqueda de Einstein de una teoría unificada, búsqueda que el profesor Glashow define como dura, persistente y fracasada.

La tesis de la ponencia es que tal teoría no existe (al menos de momento) y comienza por una introducción a la idea de lo que es y lo que no es una teoría científica. Naciones popperianas de predicibilidad y falsación son descritas por el ponente de manera muy clara. Para fijar ideas, da dos ejemplos de teorias científicas que superan la definición: la mecánica newtoniana y la teoría darwiniana de la evolución.

El profesor Glashow aprovecha para arremeter de forma clara contra las declaraciones desde el mundo de la iglesia católica (arzobispo de Viena concretamente) sobre la falsedad de los postulados darwinianos. Defiende la idea básica de que la ciencia no es un constructo social , y se manifiesta frente a los postulados postmodernos que afirman lo contrario.

Efectúa un repaso de los intentos unificadores de las fuerzas fundamentales, explicando el matrimonio feliz de los campos eléctricos y magnéticos por el electromagnetismo iniciada en 1810 por Oersted y culminada por Maxwell, Faraday y Lenz.

Albert Einstein no muestra mayor preocupación por el tema en su annus mirabilis, pero con la relatividad especial consigue en esa fecha unificar a Galileo con el electronagnetismo. El fallo era que su sistema de pensamiento (Teoría especial de la relatividad no valía para sistemas no inerciales, lo que hacía necesaria una generalización.

Esa generalización a sistemas no inerciales vendría años después con la teoría general. Se vuelve a explicar en este congreso que Einstein se dedicó por entero a su quimera particular, jugueteando durante décadas mientras otros hacían portentosos descubrimientos

Actualmente la búsqueda sigue insistente, teniendo en opinión de algunos su mejor adalid enla teoría de cuerdas . Según Glashow, sin embargo, la teoría de cuerdas no sólo no hace predicciones nuevas, sino que tampoco ha logrado explicar todo lo que ya conocemos, de modo que se considera muy escéptico al respecto. Ha criticado especialmente afirmaciones hechas desde el mundo de la teoría de cuerdas de este cariz: "hemos funcionado muy bien sin necesidad de ningún input experimental ".

El profesor Glashow hace una defensa de la ciencia básica con independencia de sus aplicaciones más inmediatas, mencionando una frase de Primo Levi , que viene a decir (no textualmente) que un mundo en el que tan sólo se estudia las cosas útiles sería un mundo mucho más triste y violento .

Preguntado al final de su charla por las contribuciones de Stephen Hawking de cara a conseguir una teoría de todo, contesta que las preguntas que se hace Stephen Hawking están entre las más profundas que puede hacerse la especie humana; pero es demasiado pronto. Antes hay que contestar otras más urgentes e inmediatas como la naturaleza de la materia oscura.

Einstein, annus mirabilis. Jornada 2 (4)

CUARTA CHARLA: PROF: FERNANDO FLORES (Universidad autónoma de Madrid)



Materia y forma en Einstein

Interesantísima charla sobre física de sólidos a la luz einsteniana.

Se repasa en avance de la física y la química en el siglo XIX, que no llega a aceptar la realidad de los átomos más que a nivel de constructo humano para explicar los observables hasta los trabajos de van't Hoff sobre isomerías orgánicas.

Paralelamente en la física ocurre algo parecido. Ostwald y Mach, incluso a finales del siglo no entienden que se pueda compaginar la existencia de átomos discretos con la de procesos irreversibles. Pareciera que dotando de movimientos inversos a los diversos átomos siempre podríamos llegar a las situaciones de partida, por lo que no debieran existir procesos irreversibles.

Entra Einstein en escena en 1.905 redescubriendo cosas por falta de información, o por su falta de contacto con la literatura científica del momento (!)

Su tesis de doctorado de 1.905 trata de determinar el número de Avogadro y el tamaño de las moléculas partiendo del estudio de la disolución del azucar en agua.

Obtiene valores de 4.10²³ para dicho número y de 10 A. para el tamaño molecular de la glucosa disuelta.

Se explica someramente el estudio del coeficiente de difusión y se relación con la ecuación de difusión mediante procesos markovianos, llegando al resultado de que el desplazamiento de ls moléculas (valor cuadrático medio) depende linealmente de dicho coeficiente, y obteniendo valores del orden de la micra por segundo.

Efecto fotoeléctrico.

Se hace un repaso de los motivos que obligaron a Einstein en 1905 a aceptar la existencia de cuantos de luz: la similitud entre las ecuaciones de variación de entropía de radiación y la variación de entropía por cambio de volumen en gases, lo que lleva a que la radiación se comporta como cuantos de energía, cuya energía depende de la frecuencia de radiación. (linealmetne, claro).

Esto intruduce la dualidad onda-corpúsculo en la física, que no nos ha abandonado hasta hoy.

Se sigue glosando los trabajos en Einstein sobre el calor específico de los sólidos en función de la temperatura a partir de la consideración de los átomos como osciladores armónicos en tres ejes ortogonales.

El final de la charla no puede ser más interesante: las aplicaciones en nanotecnología de todo lo anterior, especialmente la construcción de nanocircuitos para futuros ordenadores; nanotubos de carbonos, contactos metálicos monoatómicos, y la importancia creciente de las simulaciones de ordenador para saber qué pasa al nivel del nanómetro.

Se presenta la simulación de un contacto de aluminio con 45 átomos, de los que sólo 12 forman el puente del contacto, viendose que el modelo predice que los cambios de conductancia pasa por cambios bruscos dentro de otros momentos en los que la conductancia permanece constante. Todo muy diferente a lo que sucede a escala macroscópica.

En suma: lo nano es diferente, como reza otra de las charlas próximas.

Se termina con una predicción: el siglo XIX fué de la química, el XX de la física y la biología. EL XXI será de un amalgama entre la nanotecnología con la física, la biología y la química, produciendo dispositivos inteligentes nanométricos de cuyo alcance aún nada podemos saber, sino conjeturar.

Nota. Es evidente que no podré seguir a este ritmo, y las demás charlas tendrán que ser simples extractos. SI podeis leer esto es gracias a la paciencia de mi esposa, que prescinde de mi durante estos cuatro días.

Una vez más, pido perdón por las incorrecciones y apresuramientos.